n is a number and n=(p1^a) * (p2^b).Here p1 and p2 are prime.
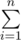 gcd(i,n)=$\sum\limits_{i=1}^{p1^a}{}gcd(i, p1a) * \sum\limits_{i=1}^{p2^b}{}$ gcd(i,p2^b) How can I prove this?
gcd(i,n)=$\sum\limits_{i=1}^{p1^a}{}gcd(i, p1a) * \sum\limits_{i=1}^{p2^b}{}$ gcd(i,p2^b) How can I prove this?
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
Math,Gcd
n is a number and n=(p1^a) * (p2^b).Here p1 and p2 are prime.
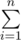 gcd(i,n)=$\sum\limits_{i=1}^{p1^a}{}gcd(i, p1a) * \sum\limits_{i=1}^{p2^b}{}$ gcd(i,p2^b) How can I prove this?
gcd(i,n)=$\sum\limits_{i=1}^{p1^a}{}gcd(i, p1a) * \sum\limits_{i=1}^{p2^b}{}$ gcd(i,p2^b) How can I prove this?
| Rev. | Язык | Кто | Когда | Δ | Комментарий | |
|---|---|---|---|---|---|---|
| en5 |

|
sahasumit288 | 2016-10-15 22:33:31 | 3 | Tiny change: 'b)\n\nHow can to prove ' -> 'b)\n\nHow to prove ' | |
| en4 |

|
sahasumit288 | 2016-10-15 22:29:28 | 2 | Tiny change: 'gcd(i,b)\nHow can ' -> 'gcd(i,b)\n\nHow can ' | |
| en3 |

|
sahasumit288 | 2016-10-15 22:28:23 | 79 | ||
| en2 |

|
sahasumit288 | 2016-10-15 22:26:07 | 3 | ||
| en1 |

|
sahasumit288 | 2016-10-15 22:25:19 | 216 | Initial revision (published) |
| Название |
|---|


