1 Bear and Game

You are supposed to implement what is described in the statement. When you read numbers t_i, check if two consecutive numbers differ by more than 15 (i.e. t_i - t_i - 1 > 15). If yes then you should print t_i - 1 + 15. You can assume that t₀ = 0 and then you don't have to care about some corner case at the beginning. Also, you can assume that t_n + 1 = 91 or t_n + 1 = 90 (both should work — do you see why?). If your program haven't found two consecutive numbers different by more than 15 then print 90. If you still have problems to solve this problem then check codes of other participants.

2 Problems for Round

Some prefix of problems must belong to one division, and the remaining suffix must belong to the other division. Thus, we can say that we should choose the place (between two numbers) where we split problems. Each pair a_i, b_i (let's say that a_i < b_i) means that the splitting place must be between a_i and b_i. In other words, it must be on the right from a_i and on the left from b_i.

For each pair if a_i > b_i then we swap these two numbers. Now, the splitting place must be on the right from a₁, a₂, ..., a_m, so it must be on the right from A = max(a₁, a₂, ..., a_m). In linear time you can calculate A, and similarly calculate B = min(b₁, ..., b_m). Then, the answer is B - A. It may turn out that A > B though but we don't want to print a negative answer. So, we should print max(0, B - A).

3 Bear and Colors

We are going to iterate over all intervals. Let's first fix the left end of the interval and denote it by i. Now, we iterate over the right end j. When we go from j to j + 1 then we get one extra ball with color c_j + 1. In one global array cnt[n] we can keep the number of occurrences of each color (we can clear the array for each new i). We should increase by one cnt[c_j + 1] and then check whether c_j + 1 becomes a new dominant color. But how to do it?

Additionally, let's keep one variable best with the current dominant color. When we go to j + 1 then we should whether cnt[c_j + 1] > cnt[best] or (cnt[c_j + 1] =  = cnt[best] and c_j + 1 < best). The second condition checks which color has smaller index (in case of a tie). And we must increase answer[best] by one then because we know that best is dominant for the current interval. At the end, print values answer[1], answer[2], ..., answer[n].

4 Bear and Two Paths

There is no solution if n = 4 or k ≤ n. But for n ≥ 5 and k ≥ n + 1 you can construct the following graph:

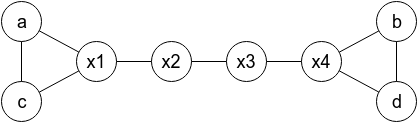
Here, cities (x1, x2, ..., x_n - 4) denote other cities in any order you choose (cities different than a, b, c, d). You should print (a, c, x1, x2, ..., x_n - 4, d, b) in the first line, and (c, a, x1, x2, ..., x_n - 4, b, d) in the second line.

Two not very hard challenges for you. Are you able to prove that the answer doesn't exist for k = n? Can you solve the problem if the four given cities don't have to be distinct but it's guaranteed that a ≠ b and c ≠ d?

5 Levels and Regions

When we repeat something and each time we have probability p to succeed then the expected number or tries is , till we succeed. How to calculate the expected time for one region [low, high]? For each i in some moment we will try to beat this level and then there will be S = t_low + t_low + 1 + ... + t_i tokens in the bag, including t_i tokens allowing us to beat this new level. The probability to succeed is 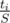, so the expected time is 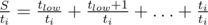. So, in total we should sum up values 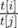for i < j. Ok, we managed to understand the actual problem. You can now stop and try to find a slow solution in O(n²·k). Hint: use the dynamic programming.

• Let dp[i][j] denote the optimal result for prefix of i levels, if we divide them into j regions.
• Let pre[i] denote the result for region containing levels 1, 2, ..., i (think how to calculate it easily with one loop).
• Let sum[i] denote the sum of t_j for all 1 ≤ j ≤ i.
• Let rev[i] denote the sum of 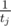for all 1 ≤ j ≤ i.

Now let's write formula for dp[i][j], as the maximum over l denoting the end of the previous region:

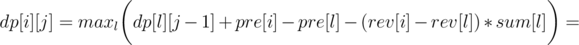
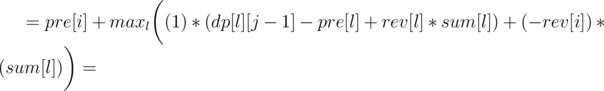
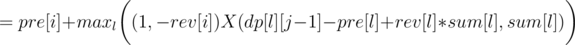
So we can use convex hull trick to calculate it in O(n·k). You should also get AC with a bit slower divide&conquer trick, if it's implemented carefully.

6 Bearish Fanpages

Let's say that every company has one parent (a company it follows). Also, every copmany has some (maybe empty) set of children. It's crucial that sets of children are disjoint.

For each company let's keep (and always update) one value, equal to the sum of:

• the income from its own fanpage
• the income from its children's fanpages

It turns out that after each query only the above sum changes only for a few values. If a starts to follows b then you should care about a, b, par[a], par[b], par[par[a]]. And maybe par[par[b]] and par[par[par[a]]] if you want to be sure. You can stop reading now for a moment and analyze that indeed other companies will keep the same sum, described above.

Ok, but so far we don't count the income coming from parent's fanpage. But, for each company we can store all its children in one set. All children have the same "income from parent's fanpage" because they have the same parent. So, in set you can keep children sorted by the sum described above. Then, we should always puts the extreme elements from sets in one global set. In the global set you care about the total income, equal to the sum described above and this new "income from parent". Check codes for details. The complexity should be 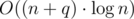, with big constant factor.

7 Bear and Destroying Subtrees

Let dp[v][h] denote the probability that subtree v (if attacked now) would have height at most h. The first observation is that we don't care about big h because it's very unlikely that a path with e.g. 100 edges will survive. Let's later talk about choosing h and now let's say that it's enough to consider h up to 60.

When we should answer a query for subtree v then we should sum up h·(dp[v][h] - dp[v][h - 1]) to get the answer. The other query is harder.

Let's say that a new vertex is attached to vertex v. Then, among dp[v][0], dp[v][1], dp[v][2], ... only dp[v][0] changes (other values stay the same). Also, one value dp[par[v]][1] changes, and so does dp[par[par[v]]][2] and so on. You should iterate over MAX_H vertices (each time going to parent) and update the corresponding value. TODO — puts here come formula for updating value.

The complexity is O(q·MAX_H). You may think that MAX_H = 30 is enough because 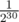is small enough. Unfortunately, there exist malicious tests. Consider a tree with 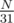paths from root, each with length 31. Now, we talk about the probability of magnitude:

which is more than 10^- 6 for d = 30.

http://www.wolframalpha.com/input/?i=1+-+(1-(1%2F2)%5Ed)%5E(N%2Fd)+for+N+%3D+500000+and+d+%3D+30

8 Bears and Juice

Let's start with O(q·p²) approach, with the dynamic programming. Let dp[days][beds] denote the maximum number of barrels to win if there are days days left and beds places to sleep left. Then:

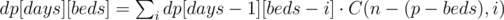
Here, i represents the number of bears who will go to sleep. If the same i bears drink from the same X barrels and this exact set of bears go to sleep then on the next day we only have X barrels to consider (wine is in one of them). And for X = dp[days - 1][beds - i] we will manage to find the wine then.

And how to compute the dp faster? Organizers have ugly solution with something similar to meet in the middle. We calculate dp for first q^2 / 3 days and later we use multiply vectors by matrix, to get further answers faster. The complexity is equivalent to O(p·q) but only because roughly q = p³. We saw shortest codes though. How to do it guys?

You may wonder why there was 2³² instead of 10⁹ + 7. It was to fight with making the brute force faster. For 10⁹ + 7 you could add sum +  = dp[a][b]·dp[c][d] about 15 times (using unsigned long long's) and only then compute modulo. You would then get very fast solution.

9 Choosing Ads

I don't know the intended solution but maybe this one in 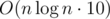would pass.

Let's say that 1/p = eps = 0.2
I need a binary tree, with 10 best candidates in each node
10 because it's 2 * (1/eps)
1) updating a tree
this one is an easier part, possible in O(q * log(n) * 10), we can go back to it later
2) answering a query about some interval
we divide the given interval into log(n) basic intervals (corresponding to some nodes in the binary tree)
we have 10*log(n) entries/candidates
pairs of integers (value, occurrences)
for each value (among at most 10*log(n) values) let's sum up occurrences from the found pairs
Note that right now we don't know the exact number of occurrences for each value. What we know is the sum of numbers of occurrences from basic intervals where the value is pretty common (at least 1/10).
I claim that we can reject many of 10*log(n) values (candidates)
for each value we DIDN'T count only some limited number of occurrences
at most INTERVAL_SIZE / 10 occurrences I think
but we are looking for values with at least INTERVAL_SIZE / 5 occurrences
so we should consider only values for which we allready counted at least INTERVAL_SIZE / 10 occurrences
and there are at most 10 of them
so we got 10 candidates
3) for each of 10 candidates I want to count the exact number of occurrences in O(log(n))
it's possible either with hashmaps in one tree
or without hashmaps with N trees, where each tree is dynamic (it has pointers and grows as we extend it)