Чтобы узнать, сколько воды вы потребляете за секунду, вы должны разделить выпитый в секунду объём v на площадь дна, равную 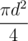 . Далее следует сравнить эту величину с e. Если ваша скорость выше, то вы опустошите кружку через
. Далее следует сравнить эту величину с e. Если ваша скорость выше, то вы опустошите кружку через 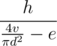 секунд. Иначе вы не сможете её опустошить.
секунд. Иначе вы не сможете её опустошить.
Для того, чтобы из набора длин можно было сложить выпуклый многоугольник, должно выполняться обобщённое неравенство треугольника: длина наибольшей стороны должна быть меньше суммы длин оставшихся сторон. Раз из текущего набора длин сложить выпуклый многоугольник невозможно, есть сторона, длина которой не меньше суммы остальных. Пусть она больше этой суммы на k; тогда достаточно добавить стержень длины k + 1. Кроме того, ясно, что никакой меньшей длиной обойтись нельзя. Таким образом, ответ на задачу~--- $\texttt{max}(l_1, \dots, l_n) — (l_1 + \dots + l_n — \texttt{max}(l_1, \dots, l_n)) + 1.
666A - Reberland Linguistics / 667C - Reberland Linguistics
Решение~--- динамическое программирование. Мы можем взять любой достаточно большой корень. Поэтому разворачиваем строку и поддерживаем dp2, 3[n]~--- можем ли мы разбить префикс длины n на строки длины 2 и 3 так, чтобы последней шла строка определённой длины. Пересчёт: 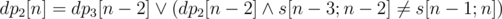 . Аналогично
. Аналогично 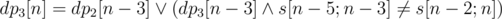 . Если dpk[n] = 1, добавляем соответствующую строку в множество ответов.
. Если dpk[n] = 1, добавляем соответствующую строку в множество ответов.
666B - World Tour / 667D - World Tour
Дан ориентированный граф, нужно найти такие 4 различные вершины a, b, c, d, что каждая последующая достижима из предыдущей и сумма кратчайших путей между соседними вершинами наибольшая. Для решения данной задачи для каждой вершины с помощью обхода в ширину посчитаем расстояния до всех остальных вершин по прямым и обратным рёбрам и сохраним три самые отдалённые вершины. После этого переберём вершины b, c, а a и d будем искать только среди трёх самых дальних по обратным рёбрам для b и трёх самых дальних по прямым рёбрам для c. Этого будет достаточно, потому что если мы зафиксировали вершины a и b, то если у нас d не из трёх самых дальних для c, мы точно сможем заменить её на одну из них и улучшить ответ.
Первое полезное наблюдение: для нас не имеет никакого значения сама строка s, а лишь её длина. В любой последовательности длины n, которая содержит заранее заданную подпоследовательность s, можно выделить её лексикографически минимальное вхождение. Оно особенно тем, что между символами ak и ak + 1 не может встретиться символ ak + 1, иначе вхождение не будет лексикографически минимальным. Обратно, если есть вхождение с таким свойством, оно будет лексикографически минимальным.
Исходя из этого, можно посчитать число строк, содержащих данную как подпоследовательность. Сначала мы выберем позиции лекс. мин. вхождения 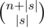 способами. Далее в любом из |s| отрезков мы можем использовать только q - 1 символов, где q -- размер алфавита, а в последнем отрезке можем взять любое слово. Иначе говоря, свободные символы слева от последнего вхождения мы выбираем из алфавита размера q - 1, а справа~--- размера q.
способами. Далее в любом из |s| отрезков мы можем использовать только q - 1 символов, где q -- размер алфавита, а в последнем отрезке можем взять любое слово. Иначе говоря, свободные символы слева от последнего вхождения мы выбираем из алфавита размера q - 1, а справа~--- размера q.
Перебирая позицию последнего символа в лекс. мин. вхождении, получаем, что таких строк 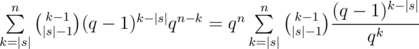 . Таким образом, если у нас фиксировано |s|, мы легко можем посчитать ответ для всех нужных n. Более того, отсюда можно вывести более простую рекуррентную формулу: пусть нам известен ответ dn для длины n. Тогда
. Таким образом, если у нас фиксировано |s|, мы легко можем посчитать ответ для всех нужных n. Более того, отсюда можно вывести более простую рекуррентную формулу: пусть нам известен ответ dn для длины n. Тогда 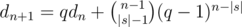 . Действительно, либо последний символ не совпадёт с последней позицией в лекс. мин. вхождении и мы пойдём по первому слагаемому, либо совпадёт, тогда мы сможем явно посчитать число таких надпоследовательностей, которое равно числу во втором слагаемом.
. Действительно, либо последний символ не совпадёт с последней позицией в лекс. мин. вхождении и мы пойдём по первому слагаемому, либо совпадёт, тогда мы сможем явно посчитать число таких надпоследовательностей, которое равно числу во втором слагаемом.
Заключительный штрих: заметим, что различных длин среди входных строк может быть лишь  , значит, решая в лоб по этой формуле, мы получим решение за
, значит, решая в лоб по этой формуле, мы получим решение за 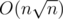 .
.
666D - Chain Reaction / 667E - Chain Reaction
В задаче даны четыре точки на плоскости. Требуется подвигать каждую из них вверх, вниз, вправо или влево, чтобы получить квадрат со сторонами, параллельными осям координат. Нужно минимизировать максимальное расстояние, на которое будет сдвинута точка.
Переберём длину стороны квадрата d, положение нижней левой точки (x, y) (среди чего перебирать, будет видно позже). Кроме того, переберём перестановку точек так, чтобы первая перешла в нижнюю левую точку квадрата, вторая — в нижнюю правую и т.д. После этого несложно проверить, действительно ли из такой перестановки точек можно получить такой квадрат, и если да, посчитать максимальное перемещение. Остаётся вопрос, где перебирать d, x и y.
Сначала определимся с d. Несложно заметить, что всегда найдутся две точки квадрата, двигающиеся по параллельным, но не совпадающим прямым. В таком случае строна квадрата~--- это расстояние между прямыми, то есть одно из чисел |xi - xj| или |yi - yj|. Это и есть множество, в котором будет перебираться d.
Чтобы понять, где перебирать x и y, переберём d из построенного выше множества и рассмотрим два случая.
\begin{enumerate} \item Есть две точки, которые двигаются по перпендикулярным прямым. Значит, в точке пересечения этих прямых есть вершина квадрата. Нижняя левая точка в каждой координате либо совпадает с ней, либо отличается на d. Точка пересечения прямых имеет координаты (xi, yj), значит, нижняя левая~--- (xi ± d, yj ± d) для некоторых i и j. Добавим все координаты xi, xi + d, xi - d в перебираемое множество. \item Все точки двигаются по параллельным прямым. Будем считать, что по горизонтальным; случай вертикальных рассматривается аналогично. Снова переберём перестановку и сдвинем каждую точку так, чтобы после своего движения она совпала с нижней левой вершиной квадрата. Вторую точку надо сдвинуть на вектор ( - d, 0), третью — на (0, - d), четвёртую — на ( - d, - d). После этого четыре точки должны оказаться на одной прямой. Теперь задачу можно переформулировать так: есть четыре точки на прямой, нужно сдвинуть их в одну точку так, чтобы минимизировать максимальный сдвиг. Несложно видеть, что сдвигать нужно в середину полученного отрезка, то есть точку (maxX - minX) / 2 (из-за требования целочисленности ответа можно округлять в любую сторону). Перебрав все перестановки, получим ещё один набор, в котором надо перебирать координату первой точки требуемого квадрата. \end{enumerate}
Дана строка s, а также m строк ti. Поступают запросы вида ``посчитать, в какой из строк с номерами из отрезка [l;r] подстрока s[a, b] встречается чаще всего''. Вообще говоря, предполагалось, что задача будет требовать online-решения, но в итоге от этой идеи было решено отказаться, поэтому её можно чисто технически комбинацией известных алгоритмов. Не будем разбирать подробно offline-решение, а сразу перейдём к online.
Построим дерево отрезков над текстами. В каждой вершине дерева построим автомат для конкатенации через разделители текстов, которые имеют номер из соответствующего вершине подотрезка и для каждого состояния в таком автомате найдём номер текста из подотрезка, в котором оно встречается наибольшее число раз, а также количество вхождений в эту позицию. Кроме того, для каждого состояния найдём состояния в детях вершины дерева отрезков, которые содержат его (если такие вообще есть). Очевидно, что все подстроки из одного состояния окажутся в одном состоянии в левой половине. В правой же половине, вообще говоря, строки, которые пересекали середину отрезка текстов могут уйти в другое состояние или исчезнуть, но это не беда. Чтобы справиться с этой проблемой, достаточно просто искать не состояние для строк, которые находятся в этом же состоянии, а состояние для строк, в которых не встречается разделитель и которые лежат в этом состоянии, так как все строки, пересекающие середину имеют вид X#Y и не интересны нам. Таким образом, для ответа на запрос, мы можем найти в корневой вершине состояние, соответствующее требуемой подстроке, а дальше спускаться по дереву, переходя в уже посчитанные переходы для состояний.
За сколько это работает? Обозначим размеры соответствующих множеств за D и X. Тогда D = C42·2 = 12. Теперь для каждого d в первом случае генерируется 4·3 = 12 координат, во втором — не более чем 4! = 24. Итого X ≤ 12·(12 + 24) = 432. Основная часть решения работает за 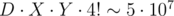 ; однако невозможно построить тест, на котором реализуются всевозможные конфигурации с движением по параллельным прямым, поэтому на самом деле перебирать придётся гораздо меньше.
; однако невозможно построить тест, на котором реализуются всевозможные конфигурации с движением по параллельным прямым, поэтому на самом деле перебирать придётся гораздо меньше.






