667A - Pouring Rain

To know how much water you consume per second you should divide consumed volume, v, by the area of the cup, 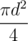. Then you should compare thisit with e. If your speed of drinking is greater, then you'll drink all the water in 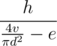seconds. Otherwise you would never do it.

667B - Coat of Anticubism

It is possible to make a convex polygon with given side lengths if and only if a generalized triangle inequality holds: the length of the longest side is less than the sum of lengths of other sides. It is impossible to make a convex polygon from a given set, so there is a side which is longest than (or equals to) than sum of others. Assume it is greater by k; then it is sufficient to add a rod of length k + 1. More, it is clear that adding any shorter length wouldn't satisfy the inequality. Thus the answer for the problem is .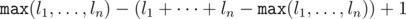

666A - Reberland Linguistics / 667C - Reberland Linguistics

This problem is solved with dynamic programming. We can select an arbitrary root of any length (at least five). Let's reverse the string. A boolean value dp_2, 3[n] denotes if we could split a prefix of length n to a strings of length 2 and 3 so that the last string has a corresponding length. Transitions: 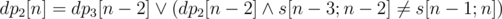. Similarly, 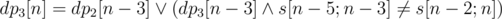. If any of dp_k[n] is true we add the corresponding string to the set of answers.

666B - World Tour / 667D - World Tour

You are given the oriented graph, find four distinct vertices a, b, c, d such that each vertex if reachable from previous and the sum of shortest paths between consequitive vertices is as large as possible. First let's run a BFS from each vertex and find three most distant vertices over given graph and its reverse. Afterwards loop through each possible b and c. Having them fixed, loop through a among three most distant vertices from b in the reversed graph and through d among three most distant vertices from c in tie initial graph. This is sufficient, because if we've fixed b and c and d is not one of three furthest from c then we could replace it with one of them and improve the answer.

666C - Codeword

The first thing to notice: string itself does not matter, only its length does. In each sequence of length n containing a fixed subsequence s we can select s's lexicographically minimal occurance, let it be p₁, ..., p_|s|. No character s_k + 1 may occur between p_k and p_k + 1 - 1, because otherwise the occurence is not lex-min. On the other hand, if there is an occurence which satsfies this criterion than it is lex-min.

Given this definition we can count number of strings containing given string as a subsequence. At first select positions of the lex-min occurance; there are 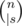ways to do it. Next, you can use any of Σ - 1 characters at first s intervals between p_i, and any of Σ at the end of the string. (Here, Σ denotes alphabet size).

Looping through p|s| — the position of last character in s in the lex-min occurence, we can count that there are exactly 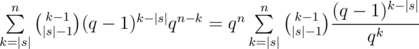strings containing s as a subsequence. So, having |s| fixed, answer for each n could be computed in linear time.

A final detail: input strings can have at most 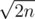different lengths. Thus simply applying the overmentioned formula we get a 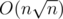solution, which was the expected one.

666D - Chain Reaction / 667E - Chain Reaction

You are given four points on the plain. You should move each of them up, down, left, or right, such that the new configuration is a square with positive integer sides parallel to coordinate axes.

Choose some d, length of the square side, and (x, y), the position of the bottom-left point. A set from where to choose will be constructed later. Then fix one of 24 permutations of initial points: first goes to the bottom-left point of the square, second goes to the bottom-right, etc. Having it fixed it is easy to check if this configuration is valid and relax the answer if needed. The only question is where to look for d, x and y.

First we deal with d. You can see that there are always two points which move among parallel but not the same lines. In this case d is the distance between these lines, i.e. one of |x_i - x_j| or |y_i - y_j|. This is the set from where d will be chosen.

Now fix d from the overmentioned set and look at two cases.

1. There are two points moving by perpendicular lines. Then there is a square vertex in the point of these lines intersection. In each coordinate this point either equals to bottom-left point of the square or differs by exactly d. Thus if bottom-left point has coordinates (x₀, y₀), than x₀ must be some of x_i, x_i + d, x_i - d, similarly for y₀. Add all this values to the set.
2. All points are moving among parallel lines; WLOG horisontal. Let's fix a permutation of points (yes, once again) and shift each point in such a way that after moving it would equal the bottom-left vertex of the square. Second point should be shifted by ( - d, 0), third by (0,  - d), fourth by ( - d,  - d). All four points must be on the same line now; otherwise this case is not possible with this permutation. Now the problem is: given four points on a line, move it to the same point minimizing the maximal path. Clearly, one should move points to the position (maxX - minX) / 2; rounding is irrelevant because of the constraint of integer answer. So, having looked through each permutations, we have another set for bottom-left vertex possible coordinates.

By the way, the 10th test (and the first test after pretests) was case 2; it was intentionally not included in pretests.

Why does it work fast? Let D and X be the sizes of corresponding lookup sets. 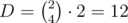. Now for each d there are 4·3 = 12 coordinates in the first case and no more than 4! = 24 in the second. Thus X ≤ 12·(12 + 24) = 432. The main part works in 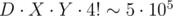; however, it is impossible to build a test where all permutations in the second case give a valid position, so you can reduce this number. Actually, the model solution solves 50 testcases in 10ms without any kind of pruning.

666E - Forensic Examination

Please, few more minutes :(