An intro would be also be kind of mainstream, but I'll still be...

Cutting to the chase

Rotations and balancing are kind of boring, but invariants are not. The nice thing about in looking for different solutions for the same problem is that you can find elegance in each of them. Maybe more importantly, it helps you develop backups when the first solution fails.

It is just the fact that sometimes to sell and start over is the right call. Of course, starting off with a small amount of one million dollars would do(couldn't help myself, people keep saying orange is the new black(now seriously: I say Donald, you say... Knuth))

Binary search tree

The problems is to implement the basic operations of a (STL's)set: * Insert * Delete * Search * Lower bound * Upper bound And so on...

The obvious slow solution is as always a list. We will try to improve it and blah, blah, blah. This is not helpful at all.

The lower and upper bounds keeps our attention. For those to be executed we need an order. A hash or whatever structure that keeps things unsorted is really hard to manage around this operation. Is the structure was static, binary search would have done the job.

From this point, I see some approaches: * leave gaps in a static structure * work with chunks of data * try to link data differently * work around binary search and make a structure that does it dynamically(that goes to BST)

I will focus on the last one, but all of them lead to interesting stuff. You can try to look up skiplists, for example.

Now, how binary works is that it looks first at the middle and then at another middle and so on. What if our structure does the exact same thing? If you draw a decision tree for a binary search, the thing that happens is that you put the middle in the top, then the middle of the left interval in left, the middle of the right interval in right and so on.

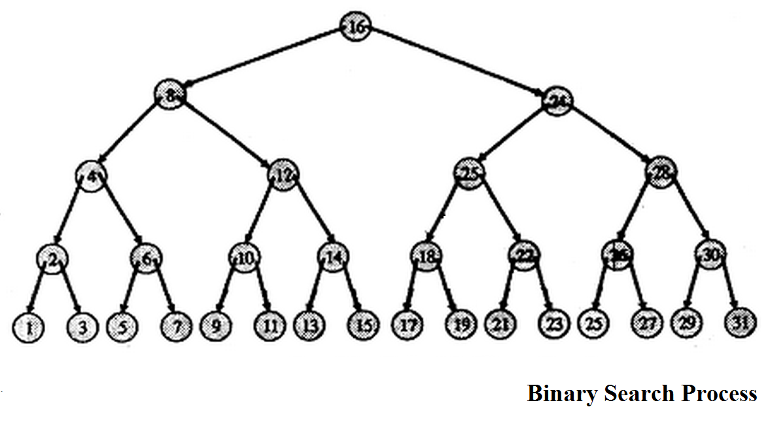
The cool things that we observe here are that: * the tree is balanced * all element in the left of a node are smaller that node and those in the right bigger

The BST is a binary tree that respects the second property.

Finding a structure that respects this property is not that hard(for example an ordered list works), but the thing that makes the decision tree above is the so called balance. Firstly, let's look why BST operations work good on average case and then try to add more invariants to make the structures good every time.

Searching

The search is straight forward. We look is the current node is what we are looking for, otherwise look in which part should we go. Here is some stolen wiki code just to be clear:

void search(Node node, int value) {
    if (!node || node.value == value) {
        return node;
    } else {
        if (node.value > value) {
            return search(node.left, value);
        } else {
            return search(node.right, value);
        }
    }
}

Insertion

Insertion goes just as the search. When we reach a null value, we insert a new node in the tree.

Node* insert(Node* node, int value) {
    if (!node) {
        return new Node(value);
    } else if (key < node->value) {
        node->left = insert(node->left, value);
    } else  
        node->right = insert(node->right, value);
    }
}

The reason we used a pointer for the node is that we want to actually modify the reference from the father of the new inserted leaf.