Modular inverse is needed to solve some Codeforces problems. Here is a particularly neat way to compute inverses in logarithmic time (in C++), which I find easier to remember than the extended Euclidean algorithm:

long long inv(long long a, long long b){
 return 1<a ? b - inv(b%a,a)*b/a : 1;
}

Here a, b are positive co-prime integers, and inv(a,b) is the inverse of a modulo b, lying between 1 and b.

The idea behind the code is that to compute inv(a,b), we find x such that and 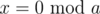, and then return x/a. To find x, we can write x = yb + 1 and solve for y by recursively computing inv(b,a). (Or actually inv(b%a, a).)

This is somewhat slower than the extended Euclidean algorithm, and you might get overflow if a*b doesn't fit inside a long long, but that shouldn't be a problem in competitions.