Мне кажется интересной традиция Endagorion дополнять разбор многих задач небольшими упражнениями, связанным с подготовкой задачи, её обобщением или наличием более эффективного решения. Попробуем и мы предложить читателю подобные вопросы по некоторым задачам.

Div. 2A (Поединок волшебников)

Автор идеи: Роман Гусарев, разработка: timgaripov.

Найдем координату первого столкновения импульсов. Они сближаются со скоростью p + q, а значит первое столкновение произойдёт через 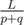секунд. Следовательно координата первого столкновения может быть вычислена как .

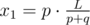Заметим теперь, что расстояние проходимое импульсами на обратном пути до волшебников равно расстоянию проходимому ими от волшебников до места первой встречи. Это значит, что импульсы вернутся к волшебникам одновременно, и ситуация станет идентична изначальной. Таким образом, вторая встреча (и все последующие) произойдёт в той же точке, что и первая.

Div. 2B (Ребрендинг)

Автор идеи: glebushka98, разработка: thefacetakt.

Тривиальное решение: будем эмулировать работу дизайнеров, а именно каждый раз ходить и честно перекрашвать все x_i в y_i и наоборот. Работает за 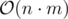, получает TL.

Попробуем улучшить этот результат.

Заметим, что одинаковые буквы переходят в одинаковые. Это означает, что позиция буквы никак не влияет на результат, и достаточно помнить для каждого возможного значения символа, во что он перейдёт. Пусть result(i, c)~--- символ, который будет стоять вместо всех вхождений c после обработки i дизайнеров. Тогда: \begin{itemize} \item result(0, c) = c \item Если result(i - 1, c) = x_i, то result(i, c) = y_i \item Аналогично, если result(i - 1, c) = y_i, то result(i, c) = x_i \end{itemize}

Данное решение работает уже за O(Σ·m + n) и проходит все тесты.

Упражнение: доведите решение данной задачи до сложности O(Σ + n + m).

Div. 2C\Div. 1A (Медианное сглаживание)

Автор идеи и разработчик: Sender.

Назовём статичными точками позиции, которые не могут измениться, сколько бы раз мы не применяли к последовательности алгоритм медианного сглаживания. Оба конца являются статичными точками по определению. Также, легко заметить, что если рядом стоят два одинаковых символа, то обе эти позиции так же являются статичными точками.

Исследуем влияние статичных точек на соседние элементы. Пусть a_i - 1 = a_i, то есть элемемнты i - 1 и i являются статичными точками. Пусть также a_i + 1 статичной точкой пока не является, следовательно a_i + 1 ≠ a_i и a_i + 1 ≠ a_i + 2. Из предыдущего предложения и того, что возможны только 0 и 1 делаем вывод, что a_i = a_i + 2 и после одного применения алгоритма медианного сглаживания будет выполнено a_i = a_i + 1. То есть любая статичная точка за один шаг превращает все сосдение элементы в статичные точки. Таким образом, любая последовательность в итоге стабилизируется.

Остаётся только вычислить скорость стабилизации и результирующие значения. Заметим, что если между двумя статичными точками i и j нет других статичных точек, то это означает чередование всех символов между позициями i и j. Несложно проверить, что в чередующейся последовательности новые статичные точки не образуются, следовательно последовательность будет оставаться чередующейся пока до неё не дойдёт влияние одной из соседних статичных точек.

Итоговое решение: выделим все статичные точки в изначальной последовательности и найдём max(min(|i - s_j|)), где s_j — множество индексов позиций статичных точек. Сложност решения O(n).

Упражнение: взломайте решение честно моделирующее применение алгоритма медианного сглаживания до стабилизации процесса.

Div. 2D\Div. 1B (Чип и Дейл спешат на помощь) ------------------ Автор идеи и разработчик: StopKran.

Div. 2E\Div. 1C (Три государства)

Автор идеи и разработчик: haku.

Div. 1D, (Сверхсекретное задание)

Автор идеи и разработчик: glebushka98.

Div. 1E (День рождения)

Автор идеи: meshanya, разработчик: romanandreev.