Problm 1 : Raising Bacteria
Write down x into its binary form. If the ith least significant bit is 1 and x contains n bits, we put one bacteria into this box in the morning of (n + 1 - i)th day. Then at the noon of the nth day, the box will contain x bacteria. So the answer is the number of ones in the binary form of x.
Problem 2 : Finding Team Member
Sort all possible combinations from high strength to low strength. Then iterator all combinations. If two people in a combination still are not contained in any team. then we make these two people as a team.
Problem 3 : A Problem about Polyline
If point (a,b) is located on the up slope/ down slope of this polyline. Then the polyline will pass the point (a - b,0)/(a + b,0).(we call (a - b) or (a + b) as c afterwards) And we can derive that c / (2 * x) should be a positive integer. Another condition we need to satisfy is that x must be larger than or equal to b. It’s easy to show that when those two conditions are satisfied, then the polyline will pass the point (a,b).
Formally speaking in math : Let c / (2 * x) = y Then we have x = c / (2 * y) ≥ b and we want to find the maximum integer y. After some more math derivation, we can get the answer is 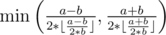 . Besides, the only case of no solution is when a < b.
. Besides, the only case of no solution is when a < b.
In fact, 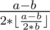 always dosn't exist or larger than
always dosn't exist or larger than 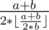 .
.
author's code:
#include <bits/stdc++.h>
typedef long long LL;
using namespace std;
int main(){
LL a,b;
cin>>a>>b;
if(a<b)puts("-1");
else printf("%.12f\n",(a+b)/(2.*((ab)/(2*b))));
return 0;
}
Problem 4 : Or Game
We can describe a strategy as multiplying ai by x ti times so ai will become bi = ai * xti and sum of all ti will be equals to k. The fact is there must be a ti equal to k and all other ti equals to 0. If not, we can choose the largest number bj in sequence b, and change the strategy so that tj = k and all other tj = 0. The change will make the highest bit 1 of bj become higher so the or-ed result would be higher.
After knowing the fact, We can iterator all number in sequence a and multiply it by xk and find the maximum value of our target between them. There are several method to do it in lower time complexity. You can check the sample code we provide.(I believe you can understand it quickly.)
author's code:
#include<cstdio>
#include<algorithm>
using namespace std;
const int SIZE = 2e5+2;
long long a[SIZE],prefix[SIZE],suffix[SIZE];
int main(){
int n,k,x;
scanf("%d%d%d", &n, &k, &x);
long long mul=1;
while(k--)
mul *= x;
for(int i = 1; i <= n; i++)
scanf("%I64d", &a[i]);
for(int i = 1; i <= n; i++)
prefix[i] = prefix[i-1] | a[i];
for(int i = n; i > 0; i--)
suffix[i] = suffix[i+1] | a[i];
long long ans = 0;
for(int i= 1; i <= n; i++)
ans = max(ans, prefix[i-1] | (a[i] * mul) | suffix[i+1]);
printf("%I64d\n",ans);
}
Problem 5 : Weakness and Poorness
Let 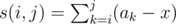 , we can write down the definition of poorness formally as
, we can write down the definition of poorness formally as
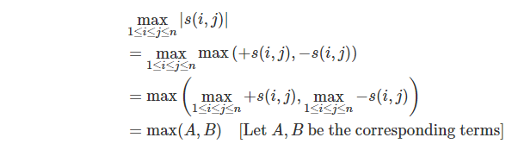
. It's easy to see that A is a strictly decreasing function of x, and B is a strictly increasing function of x. Thus the minimum of max(A, B) can be found using binary or ternary search. The time complexity is 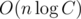 ,
,
Now here give people geometry viewpoint of this problem:
let 
We plot n + 1 straight line y = i * x + bi in the plane for i from 0 to n.
We can discover when you are given x. The weakness will be (y coordinator of highest line at x) — (y coordinator of lowest line at x).
So we only need to consider the upper convex hull and the lower convex hull of all lines. And the target x value will be one of the intersection of these convex hull.
Because you can get these line in order of their slope value. we can use stack to get the convex hulls in O(n).
author's code : this (using binary search)
code of author's friend (using stack to handle convexhull with O(n), have more precision)
Problem 6 : LCS again
Followings are solution in short. Considering the LCS dp table lcs[x][y] which denotes the LCS value of first x characters of S and first y characters of T. If we know lcs[n][n] = n - 1, then we only concern values in the table which abs(x - y) ≤ 1 and all value of lcs[x][y] must be min(x, y) or min(x, y) - 1. So each row contains only 8 states(In fact,three states among these states will never be used), we can do dp on it row by row with time complexity O(n).
author's code:
#include <bits/stdc++.h>
#define SZ(X) ((int)(X).size())
#define ALL(X) (X).begin(), (X).end()
#define REP(I, N) for (int I = 0; I < (N); ++I)
#define REPP(I, A, B) for (int I = (A); I < (B); ++I)
#define RI(X) scanf("%d", &(X))
#define RII(X, Y) scanf("%d%d", &(X), &(Y))
#define RIII(X, Y, Z) scanf("%d%d%d", &(X), &(Y), &(Z))
#define DRI(X) int (X); scanf("%d", &X)
#define DRII(X, Y) int X, Y; scanf("%d%d", &X, &Y)
#define DRIII(X, Y, Z) int X, Y, Z; scanf("%d%d%d", &X, &Y, &Z)
#define RS(X) scanf("%s", (X))
#define CASET int ___T, case_n = 1; scanf("%d ", &___T); while (___T-- > 0)
#define MP make_pair
#define PB push_back
#define MS0(X) memset((X), 0, sizeof((X)))
#define MS1(X) memset((X), -1, sizeof((X)))
#define LEN(X) strlen(X)
#define PII pair<int,int>
#define VPII vector<pair<int,int> >
#define PLL pair<long long,long long>
#define F first
#define S second
typedef long long LL;
using namespace std;
const int MOD = 1e9+7;
const int SIZE = 1e5+10;
// template end here
LL dp[SIZE][8];
char s[SIZE];
int get_bit(int x,int v){return (x>>v)&1;}
int main(){
DRII(n,m);
RS(s+1);
REPP(i,1,n+1)s[i]-='a';
s[n+1]=-1;
REP(i,m){
int state=1;
if(i==s[1])state|=2;
if(i==s[1]||i==s[2])state|=4;
dp[1][state]++;
}
REPP(i,2,n+1){
REP(j,8){
int d[4]={i-3+get_bit(j,0),i-2+get_bit(j,1),i-2+get_bit(j,2)};
REP(k,m){
int d2[4]={};
REPP(l,1,4){
if(s[i-2+l]==k)d2[l]=d[l-1]+1;
else d2[l]=max(d2[l-1],d[l]);
}
if(d2[1]>=i-2&&min(d2[2],d2[3])>=i-1)dp[i][(d2[1]-(i-2))|((d2[2]-(i-1))<<1)|((d2[3]-(i-1))<<2)]+=dp[i-1][j];
}
}
}
printf("%lld\n",dp[n][0]+dp[n][1]+dp[n][4]+dp[n][5]);
return 0;
}
Problem 7 : Walking!
Since there is only one person, it’s not hard to show the difference between the number of left footprints and the number of right footprints is at most one.
For a particular possible time order of a sequence of footprints, if there are k backward steps, we can easily divide all footprints into at most k + 1 subsequences without backward steps. Then you might guess that another direction of the induction is also true.That is, we can combine any k + 1 subsequence without backward steps into a whole sequence contains at most k backward steps. Your guess is correct !
Now we demostrate the process of combining those subsequences.
We only concern the first step and the last step of a divided subsequence. There are four possible combinations, we denote them as LL/LR/RL/RR subsequence separately(the first character is the type of the first step and the second character is the type of the second step).
Suppose the number of four types of subseueqnce(LL/LR/RL/RR) are A, B, C, D separately. We have abs(A - D) ≤ 1.
We can combine all RR, LL subsequeces in turn into one subsequenceswith at most A + D - 1 backward steps(the result may be of any of the four subsquence types). Now we have at most one LL or RR type subsequence.
Then we can combine all RL subsequence into only one RL subsequence with at most A - 1 backward steps easily. And so do LR subsequences. Now we want to combine the final RL and LR subsequences together. We could pick the last footprint among two subsequences, exclude it from the original subsequcne and append it at the tail of another subsequence. The move will not increase the number of backward step and the types of the two subsequences would become RR and LL ! We can easily combine them into one LR or RL subsequence now. If there is still a LL or RR type subsequence reamained. We can easily combine them, too.
So if we can divide all footprints into the least number of subsequences without backward steps. Then we have solved the problem. And this part can be done with greedy method.
Following provide one possible greedy method:
The method will come soon...
Problem 8 : The Mirror Box
If we view the grid intersections alternatively colored by blue and red like this:
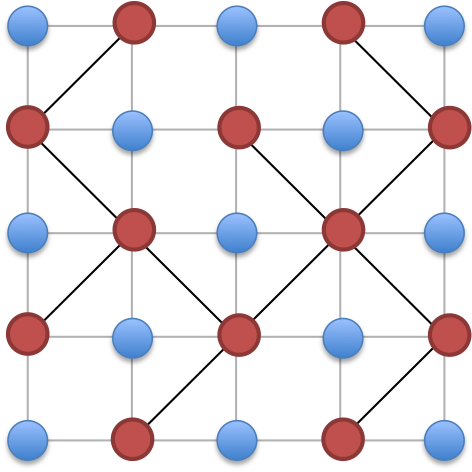
Then we know that the two conditions in the description are equivalent to a spanning tree in either entire red intersections or entire blue dots. So we can consider a red spanning tree and blue spanning tree one at a time.
We can use disjoint-sets to merge connected components. Each component should be a tree, otherwise some grid edges will be enclosed inside some mirrors. So for the contracted graph, we would like to know how many spanning trees are there. This can be done by Kirchhoff’s theorem.
Since there are at most 200 broken mirrors, the number of vertices in the contracted graph should be no more than 201. Hence a O(|V|3) determinant calculation algorithm may be applied onto the matrix.





