Отсортируем все дома по координате на оси OX (сохраняя их относительную нумерацию для вывода ответа). Далее можно сделать очевидный вывод — наибольшей стоимостью отправки письма из i-го города будет являться максимум из расстояний от i-го города до первого и от i-го города до последнего (max(abs(xi - x0), abs(xi - xn - 1)). А минимальной стоимостью отправки будет являться минимум из расстояний до соседних городов (для i-го города соседними являются города с номерами i - 1 и i + 1), то есть (min(abs(xi - xi - 1), abs(xi - xi + 1)). Для всех городов, кроме самого левого и самого правого, это считается нормально. Так как у самого левого нет соседей левее, значит минимальная стоимость определяются однозначно (abs(xi - xi + 1)). Аналогично для самого правого города (abs(xi - xi - 1)).
567B - Berland National Library
Чтобы корректно обрабатывать события, нам необходимо знать, находится ли в библиотеке на данный момент человек. Для этого будем использовать массив in типа bool. Также заведём две переменные для хранения ответа и "текущего состояния" (в которой будет храниться количество человек, присутствующих в библиотеке на данный момент). Их обозначим ans и state соответственнно.
Итак, если к нам поступает запрос вида " + ai", то мы увеличиваем state на единицу, отмечаем, что этот человек зашёл в читальный зал (in[ai] = true) и пытаемся обновить ответ (ans = max(ans, state)).
Иначе же к нам поступает запрос вида " - ai". В данном случае если человек, который выходит из библиотеки, находился в ней, то нам просто нужно уменьшить state. Иначе мы понимаем, что если этого человека "не было" в библиотеке (in[ai] == false) и он выходит, значит он был в читальном зале ещё до начала рассматриваемого нами промежутка времени. Тогда мы в любом случае должны увеличить ответ на единицу. Также не стоит забывать, что необходимо отметить, что человек вышел из библиотеки (in[ai] = false).
Давайте будем решать эту задачу относительно фиксированного среднего элемента. Это значит, что если мы фиксируем элемент ai, то наша прогрессия должна состоять из элементов вида ai / k, ai, ai·k. Заметим, что прогрессии со средним элементом ai не будет существовать, когда ai не делится нацело на k (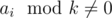 ).
).
При фиксированном среднем члене мы сможем отвечать на запрос вида "сколько существует подпоследовательностей — геометрических прогрессий, средний элемент которых стоит строго в позиции i". Очевидно, что это будет количество элементов слева от i-го, равных ai / k, умноженное на количество элементов, находящихся справа от i-го, равных ai·k. То есть мы можем отвечать на этот вопрос для каждого элемента, если будем знать количества элементов слева и справа от i-го. Для этого можно использовать ассоциативный массив (map). Будем хранить 2 map-a l и r, в l будем поддерживать все элементы строго левее i-го, а в r — строго правее i-го. Если идти по массиву слева направо, то l должен быть пустым, а в r должны быть все элементы. Пройдём циклом по всему изначальному массиву, постепенно обновляя map-ы (очевидно, что перед рассмотрением i-го элемента мы должны удалить его из r, а после рассмотрения — добавить его в l). Если ai будет делиться нацело на k, то добавляем к ответу l[ai / k] * r[ai * k] (стоит заметить, что как при перемножении, так и при обновлении ответа могут случаться переполнения типа int, поэтому проще всего все переменные хранить в long long).
567D - One-Dimensional Battle Ships
Сначала нам необходимо понять, в каком случае мы можем утверждать, что Алиса соврала. Это случится, когда на поле размера n невозможно будет уместить k кораблей размера a. Для отрезка фиксированной длины len мы можем посчитать максимальное количество кораблей размера a, которые могут уместиться на таком поле. Каждый корабль занимает ровно a + 1 клетку, кроме одного крайнего. Поэтому для отрезка длины len формула для подсчёта будет выглядеть так: 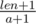 (чтобы не учитывать корабль, который занимает a клеток, а не a + 1, мы просто добавим одну <<фиктивную>> клетку в наш отрезок). Значит, для отрезка [l..r] наша формула должна выглядеть так:
(чтобы не учитывать корабль, который занимает a клеток, а не a + 1, мы просто добавим одну <<фиктивную>> клетку в наш отрезок). Значит, для отрезка [l..r] наша формула должна выглядеть так: 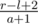 .
.
Для решения задачи нам надо хранить все отрезки [l..r], внутри которых все клетки "свободны" (то есть ни в одну из клеток отрезка не было произведено выстрела). Для удобства их можно хранить в множестве (std: : set), чтобы можно было легко найти нужный отрезок. Итак, будем обрабатывать выстрелы по очереди. Изначально количесво помещающихся кораблей будет равняться 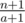 (это значит, что у нас есть один отрезок [1..n]). После каждого выстрела один из отрезков будет либо делиться на два отрезка меньшего размера, либо он будет просто уменьшаться в размере на единицу (если выстрел будет произведён в его край). Таким образом, если выстрел произведён в точку x, относящуюся к отрезку [l..r], то мы должны вычесть из нашего общего количества кораблей их количество на отрезке [l..r], удалить этот отрезок из множества и разделить его на два новых: [l..x - 1] и [x + 1..r] (если выстрел был произведён в край отрезка, тогда добавляется только один новый отрезок) и прибавить к количеству
(это значит, что у нас есть один отрезок [1..n]). После каждого выстрела один из отрезков будет либо делиться на два отрезка меньшего размера, либо он будет просто уменьшаться в размере на единицу (если выстрел будет произведён в его край). Таким образом, если выстрел произведён в точку x, относящуюся к отрезку [l..r], то мы должны вычесть из нашего общего количества кораблей их количество на отрезке [l..r], удалить этот отрезок из множества и разделить его на два новых: [l..x - 1] и [x + 1..r] (если выстрел был произведён в край отрезка, тогда добавляется только один новый отрезок) и прибавить к количеству 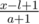 и
и 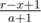 (соответственно, если появляется только один новый отрезок, то необходимо прибавить только одну величину).
(соответственно, если появляется только один новый отрезок, то необходимо прибавить только одну величину).
Если после обработки какого-то из выстрелов количество кораблей стало меньше, чем k, то это означает, что Алиса соврала нам, выводим номер этого хода. Если же после обработки всех выстрелов количество кораблей так и осталось не меньше, чем k, выводим <<-1>>.
Сначала давайте разберёмся, какие рёбра не будут лежать ни на одном кратчайшем пути из s в t. Если запустить два алгоритма поиска кратчайших путей (из вершины s и из вершины t) и сохранить расстояния в массивах d1 и d2 соответственно, можно сделать следующий вывод: если у нас есть ребро (u, v), то оно будет лежать хотя бы на одном кратчайшем пути из s в t тогда и только тогда, когда d1[u] + w(u, v) + d2[v] == d1[t] (где w(u, v) — вес ребра (u, v)).
После того, как мы построили граф кратчайших путей из s в t, мы можем определить, какие из рёбер лежат на всех кратчайших путях. Если представить путь из s в t в виде отрезка [0..D], а расстояния между парами вершин, соединённых рёбрами в этом графе, в виде подотрезков данного отрезка (например, если у нас есть ребро (u, v), тогда данный подотрезок будет иметь вид [d1[u]..d1[v]]), то можно заметить, что все подотрезки каким-то образом касаются других подотрезков (некоторые также могут пересекаться с другими подотрезками). Ребро (u, v) будет лежать на всех кратчайших путях из s в t, если подотрезок [d1[u]..d1[v]] будет только касаться других подотрезков (внутренние пересечения с другими подотрезками недопустимы). Теперь мы можем однозначно отвечать "YES" для этих рёбер.
Остальная часть задачи более простая. Если ребро (u, v) с весом w не лежит на всех кратчайших путях, можно попробовать уменьшить его. Данное ребро будет лежать на всех кратчайших путях только в том случае, если его вес станет равен d1[u] - d2[v] - 1. Итак, если величина d1[t] - d1[u] - d2[v] - 1 (предполагаемый новый вес нашего ребра)строго положительна, тогда мы сможем уменьшить наше ребро так, чтобы оно лежало на всех кратчайших путях, выведем "CAN" и через пробел разность между старым и новым весами ребра. Иначе же выведем "NO".
Представим, что мы выставляем блоки по парам в порядке возрастания их высоты, начиная с левого и правого края. Так, например, два блока высоты 1 мы можем поставить в позиции 1 и 2, либо в позиции 1 и 2n, либо в позиции 2n - 1 и 2n. Отрезок незанятых мест таким образом изменится, и следующая по высоте пара блоков будет выставляться уже в образовавшиеся крайние позиции. В конце концов останутся две свободные позиции, куда необходимо поставить пару блоков высоты n.
Очевидно, вышеописанным способом строится любая корректная последовательность. Попробуем посмотреть на требования к высотам блоков со стороны такого способа построения последовательности. Поскольку блоки мы выставляем в порядке возрастания высот, то неравенства теперь ставят ограничения только на порядок расстановки блоков. Например, требование ''3 >= 5'' теперь означает, что ставить блок в позицию 3 мы можем только лишь если блок в позиции 5 уже поставлен (а значит он имеет меньшую высоту), или же в позициях 3 и 5 блоки нужно ставить одновременно (пара блоков одной высоты).
Для дальнейшего подсчета количества способов воспользуемся идеей динамического программирования. Будем считать dp[l][r] — количество способов поставить блоки, если свободные от блоков места образуют отрезок [l, r]. Высота пары блоков, которая будет ставится в крайние места отрезка однозначно определяется границами этого отрезка. Переберем один из трех вариантов расстановки очередной пары блоков (исключение составляет случай l = = r + 1). Теперь проверим, что такая расстановка не нарушает требования условия задачи. Будем рассматривать только ограничения, касающиеся позиций, на которые ставятся блоки в фиксированном варианте. Для любой "текущей" позиции должно выполняться "<" для любого еще не занятого места (которое находится внутри отрезка [l, r], но не совпадает с одним из двух "текущих" мест), ">" для любого занятого места (вне [l, r]), а ''='' выполняться только в случае сравнения двух "текущих" мест.
Такое динамическое программирование проще всего считать рекурсивно, "ленивой" динамикой.







