In this post I'll try to expose the results of my research regarding the rating formula. More specifically, I'll show a graph that gives you a rating according to your performance and I'll show the basic aspects of how ratings are updated. This post is quite large, if you are only interested in the results you can easily skim through it :)
Motivation
Almost two years ago I started to participate in contests more actively, aiming to be red one day. To increase my motivation I tried to find a formula that evaluated how well I did during a competition. At that time there were no API nor [user:DmtryH]'s statistics so I manually looked at a lot of profiles to try to find 'stable' points: users that didn't change their rating after a competition. Supposing that, in that case, they performed as they were expected; I obtained two approximate linear formulas for Div-1 contests:
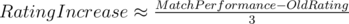
The 1st formula was a linear approximation of a non-linear function, it started to fail roughly for red performances. The second one works pretty bad, but it can give you an idea of how much it will increase. With this I did an Excel like this one:

As you can see the colours in the left look much more interesting than the colours on the right. For instance, in one contest my rating was >2500, which (obviously) gave me a boost in motivation; next contest I performed 1000 points lower; which surprisingly motivated me as well to do a Virtual Contest and get back on track.
As months progressed I saw that this formula was helping me and could help others as well, so, as an extra motivation, I promised myself that when I first turned red I would do a serious post about it (and also write a CF contest for both divisions (separately), if they allow me :) ). I may not be red when you read this post; but,anyway, here it goes!
Theoretical analysis
The basis of my work is MikeMirzayanov's blog, along with some others. In CF, the probability that A wins B in terms of their rating is:
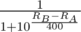
The theory of the ELO system suggests that, after a match, ratings of A and B should be updated by a constant multiplied by the difference between the expected result and the actual result.
Now, we can just run all the 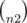 matches between the contestants, if we add the probabilities of winning against every participant we get the expected rank (+0.5 because ranks start with 1 and the probability of winning against yourself is 0.5), thus:
matches between the contestants, if we add the probabilities of winning against every participant we get the expected rank (+0.5 because ranks start with 1 and the probability of winning against yourself is 0.5), thus:
Unable to parse markup [type=CF_TEX]






