In this problem we can get AC with many solutions:
1) With every new rectangle we will add his area to the result, so for each line x1, y1, x2, y2 we will add to answer (x2 - x1 + 1) * (y2 - y1 + 1)
Time complexity O(n).
2) We can just do all, that is written in the statement: create an array and with each new rectangle we can just increment every element inside rectangle. In the end we can just add all elements inside this array.
Time complexity O(n * x * y)
We can find out a formula for this problem:
for n < 10 answer will be n = n - 1 + 1 = 1 * (n + 1) - 1;
for n < 100 answer will be 2 * (n - 9) + 9 = 2 * n - 9 = 2 * n - 10 - 1 + 2 = 2 * (n + 1) - 11;
for n < 1000 answer will be 3 * (n - 99) + 2 * (99 - 9) + 9 = 3 * n - 99 - 9 = 3 * n - 100 - 10 - 1 + 3 = 3 * (n + 1) - 111;
so for n < 10sz answer will be 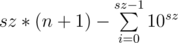 ;
;
Time complexity O(sz), where sz is the length of n.
We also could just try 10 options n < 10, n < 100, ..., n < 109, n = 109 and solve problem for each option.
UPD: Don't use function pow() to find powers of 10, because it doesn't work right sometimes.
Convert m to number system of base w. If all digits of number – 0 or 1, then we can measure the weight of the item with putting weights, that have digits equal to 1, on one pan, and our item on another one.
If this condition isn't satisfied, then we should iterate from lower digit to high and if digit is not equal to 0 or 1, we try to substract w from it and increment higher digit. If it becomes equal to - 1, then we can put weight with number of this digit on the same pan with our item, if it becomes equal to 0, then we don't put weight, in another case we can't measure the weight of our item and answer is  .
.
Time complexity O(logm).
We can look through all pair of points, draw line through each pair and write, that this line includes these 2 points. We can do it with map. If some line includes x points, then in fact we counted, that it has 2 * x * (x - 1) points, because we included each point 2*(x-1) times in this line.
We can create an array and add to him values b[2 * x * (x - 1)] = x, so we can define, how many points is on the line. Then we can iterate through all lanes and for each line with x points we will loose x * (x - 1) * (x - 2) / 6 possible triangles from all possible n * (n - 1) * (n - 2) / 6 triangles. Decide, that at first ans = n * (n - 1) * (n - 2) / 6. So for every line, that includes x points, we will substract x * (x - 1) * (x - 2) / 6 from ans.
Time complexity O(n2 * logn).
UPD: I am sorry, that O(n3 / 6) solutions passed, my solution with O(n3 / 6) didn't pass before the contest, so I decided, that TL 4 sec is good(it was for Java TL).
We can see, that we can reach maximal answer, when brackets will be between two signs * , or between one sign * and the end of expression. For convenience we will add in the begin of expression 1 * , and in the end of expression * 1.
After that we can iterate all possible pairs of signs * and count the expression with putting brackets between two signs * for each pair.
We can use two variables x and y to count the value of expression, in the begin x = 0, y = firstnumber, where firstnumber is first digit of expression, then if next sign is + , then x = y, y = nextnumber, and if next sign is * , then x = x, y = y * nextnumber. The value of expression will be x + y, we can create function, like that, to count expressions inside and outside the brackets.
Time complexity O(|s| * 172).
P.S. Sorry for my bad english, I will try to correct mistakes in the near time.







