When finding the contribution of a straight line in a problem and seeking the maximum or minimum value, some targeted algorithms are usually used to solve it. If you find a contribution formula related to the straight line formula and need to find the maximum or minimum value among the contribution values, consider the following algorithms.
1. Li Chao Segment Tree
1. Algorithm Explanation
The Li Chao segment tree is a data structure for handling straight line problems derived from the segment tree. The operations it can handle are:
- Query the maximum or minimum value at a single point;
- Add a straight line to an interval.
We build a segment tree for the interval (a segment tree with dynamic node creation is more common). Each node stores only one straight line (slope + intercept). For a single-point query, we traverse the points on the path from the root to the leaf node corresponding to the subscript, calculate the results corresponding to the stored straight lines, and make contributions. For adding a straight line, first find the corresponding nodes on the segment tree for the interval where the straight line is located, and then update a single node to be updated according to the following operations:
- This node retains the straight line with the better value at the midpoint of the interval and passes the other straight line down.
- If the straight line to be passed down is better at the left boundary of the interval, it is used to update the left child.
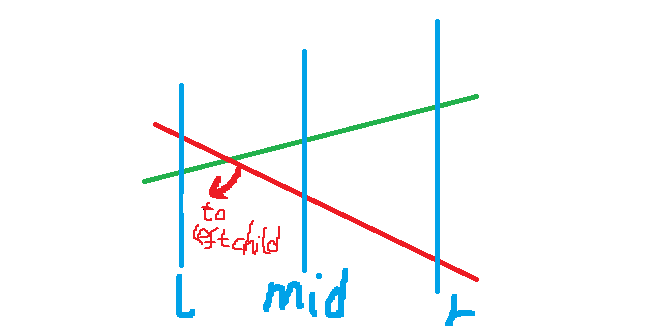
- If the straight line to be passed down is better at the right boundary of the interval, it is used to update the right child.
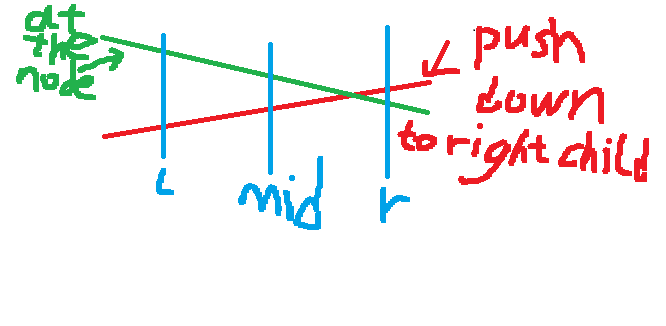
- If a vertically upward straight line appears, it is generally processed as a straight line with a slope of 0 and an intercept equal to the optimal point on the straight line.
It can be found that at most one of the operations in $$$2$$$ and $$$3$$$ will update the child. It can be concluded that the worst-case time complexity for a single-point update is $$$\operatorname{O}(\log_2 n)$$$. Any interval will correspond to $$$\operatorname{O}(\log_2 n)$$$ nodes, and the time complexity for adding a straight line to any interval is $$$\operatorname{O}(\log_2^2 n)$$$. However, when optimizing the straight line transfer, mostly only global addition is used, and only the root node needs to be updated, resulting in a time complexity of $$$\operatorname{O}(\log_2 n)$$$.
2. Advantages
- Easy to use: Optimizing the straight line transfer with the Li Chao segment tree does not require ensuring the monotonicity of the straight line slope. It is straightforward to apply in implementation and supports persistence, merging, and splitting of the segment tree. When the number of operations is limited, it can be brutally cleared, which is very useful.
- Code difficulty: The template of the Li Chao segment tree is similar to that of the segment tree. It is very simple for contestants who have mastered the segment tree proficiently. And the segment tree is a high-frequency knowledge point in competitions at the advanced level and above. Therefore, the code difficulty is not high for many contestants.
- Efficiency: Compared with the CDQ divide-and-conquer method, the Li Chao segment tree is in most cases $$$\operatorname{O}(\log_2 n)$$$ times faster in efficiency.
3. Limitations
Using the Li Chao segment tree requires ensuring that the number of points for which the optimal value is sought is limited when the straight line formula makes contributions, and it cannot support deletion.
4. Problem
2. Monotonic Queue and Convex Hull
For the situation where the slopes of the straight lines added are monotonically non-deteriorating in the order of addition and the query coordinates are monotonically increasing, consider using a monotonic queue to obtain:
- When adding to the end of the queue, consider the magnitude of the abscissa of the intersection point of the added straight line and the last straight line and the abscissa of the intersection point of the last straight line and the previous straight line. If the former is smaller, delete the last straight line.
- If the contribution of the straight line at the head of the queue is worse than that of the next one, delete the head of the queue.
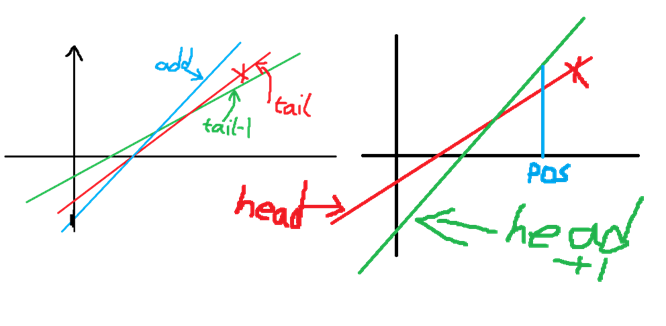
Operation $$$1$$$ is continuously performed before insertion until the last element does not meet the deletion condition. Operation $$$2$$$ is continuously performed before insertion until the head of the queue does not meet the addition condition. In this way, we obtain a linear solution for this type of straight line transfer problem. If we explain the problem in another way: - Insert nodes, and the abscissas are monotonically increasing; - Query the intercept of the straight line with the largest slope passing through one of the points.
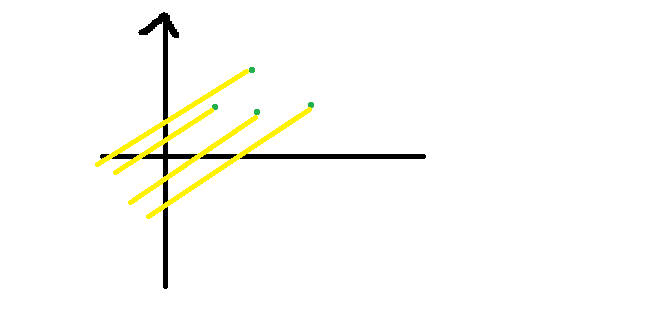
Then the solution is the convex hull. Also, maintain a double-ended queue. When inserting, delete the end of the queue when it is found to turn upward.
The two methods have different explanations but the same essence. You can choose according to your preference. For the situation where the query points are not necessarily monotonically increasing, consider not deleting the head of the queue and perform a binary search during the query, which will add an additional $$$\operatorname{O}(\log_2 n)$$$. For the situation where the slopes of the straight lines are not necessarily monotonically increasing, consider adding the CDQ divide-and-conquer method. Sort the left half according to the slope each time to update the right half, and the time complexity is $$$\operatorname{O}(n\log_2^2 n)$$$.
Advantages
- Code difficulty: The queue part is easy to write, and the CDQ divide-and-conquer is not difficult to write either;
- Efficiency: The insertion and deletion of the queue are amortized linearly.
Disadvantages
For the situation that requires the CDQ divide-and-conquer method, it needs to be offline, and it may be inconvenient to apply for complex problems.
Example Problem
Summary
Different algorithms have different advantages and disadvantages, and different algorithms should be used for different situations. In the problem of the maximum or minimum contribution of a straight line, we find that the Li Chao segment tree and the monotonic queue can help us solve this problem quickly and further handle more complex dynamic programming problems.





