Hi all,
I would like to share with you a part of my undergraduate thesis on a Multi-String Pattern Matcher data structure. In my opinion, it's easy to understand and hard to implement correctly and efficiently. It's competitive against other MSPM data structures (Aho-Corasick, suffix array/automaton/tree to name a few) when the dictionary size is specifically (uncommonly) large.
I would also like to sign up this entry to bashkort's Month of Blog Posts:-)
Abstract
This work describes a hash-based mass-searching algorithm, finding (count, location of first match) entries from a dictionary against a string $$$s$$$ of length $$$n$$$. The presented implementation makes use of all substrings of $$$s$$$ whose lengths are powers of $$$2$$$ to construct an offline algorithm that can, in some cases, reach a complexity of $$$O(n \log^2n)$$$ even if there are $$$O(n^2)$$$ possible matches. If there is a limit on the dictionary size $$$m$$$, then the precomputation complexity is $$$O(m + n \log^2n)$$$, and the search complexity is bounded by $$$O(n\log^2n + m\log n)$$$, even if it performs in practice like $$$O(n\log^2n + \sqrt{nm}\log n)$$$. Other applications, such as finding the number of distinct substrings of $$$s$$$ for each length between $$$1$$$ and $$$n$$$, can be done with the same algorithm in $$$O(n\log^2n)$$$.
Problem Description
We want to write an offline algorithm for the following problem, which receives as input a string $$$s$$$ of length $$$n$$$, and a dictionary $$$ts = \{t_1, t_2, .., t_{\lvert ts \rvert}\}$$$. As output, it expects for each string $$$t$$$ in the dictionary the number of times it is found in $$$s$$$. We could also ask for the position of the fist occurrence of each $$$t$$$ in $$$s$$$, but the paper mainly focuses on the number of matches.
Algorithm Description
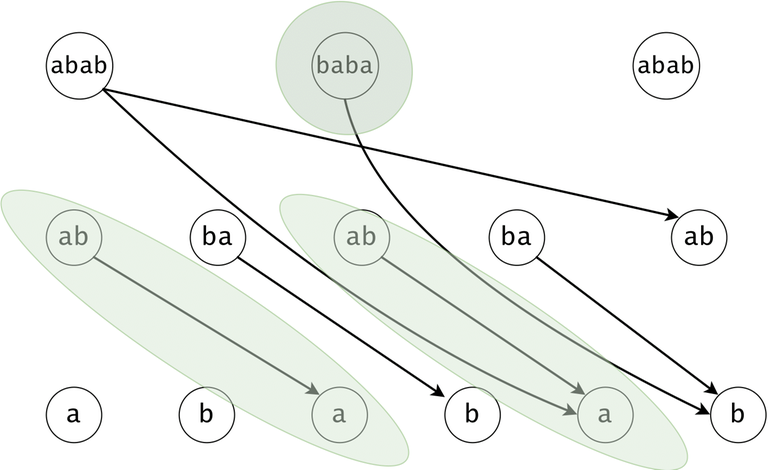
We will build a DAG in which every node is mapped to a substring from $$$s$$$ whose length is a power of $$$2$$$. We will draw edges between any two nodes whose substrings are consecutive in $$$s$$$. The DAG has $$$O(n \log n)$$$ nodes and $$$O(n \log^2 n)$$$ edges.
We will break every $$$t_i \in ts$$$ down into a chain of substrings of $$$2$$$-exponential length in strictly decreasing order (e.g. if $$$\lvert t \rvert = 11$$$, we will break it into $$$\{t[1..8], t[9..10], t[11]\}$$$). If $$$t_i$$$ occurs $$$k$$$ times in $$$s$$$, we will find $$$t_i$$$'s chain $$$k$$$ times in the DAG.