#include <bits/stdc++.h>

#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()

const char nl = '\n';
typedef long long ll;
typedef long double ld;

using namespace std;

void solve() {
    int n, k;
    cin >> n >> k;
    cout << 1 + (n - 1) * k << nl;
}

int main() {
	ios::sync_with_stdio(0); cin.tie(0);
    
    int t;
    cin >> t;
    while (t--) {
        solve();
    }
}

• Good problem
• Average problem
• Bad problem

#include <bits/stdc++.h>

#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()

const char nl = '\n';
typedef long long ll;
typedef long double ld;

using namespace std;

void solve() {
    int n;
    cin >> n;
    
    vector<int> a(n);
    for (int i = 0; i < n; i++) cin >> a[i];
    
    ll pref_max = 0, s = 0, mx = 0;
    for (int i = 0; i < n; i++) {
        pref_max = max(pref_max, (ll) a[i]);
        
        ll d = pref_max - a[i];
        s += d;
        mx = max(mx, d);
    }
    
    cout << s + mx << nl;
}

int main() {
	ios::sync_with_stdio(0); cin.tie(0);
    
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
}

• Good problem
• Average problem
• Bad problem

#include <bits/stdc++.h>

#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()

const char nl = '\n';
typedef long long ll;
typedef long double ld;

using namespace std;

void solve() {
    int n;
    cin >> n;
    
    vector<int> h(n);
    for (auto &x: h) cin >> x;
    
    int ans = h[n - 1];
    for (int i = n - 2; i >= 0; i--) {
        ans = max(ans + 1, h[i]);
    }

    cout << ans << nl;
}

int main() {
	ios::sync_with_stdio(0); cin.tie(0);
    
    int T;
    cin >> T;
    while (T--) solve();
}

• Good problem
• Average problem
• Bad problem

#include <bits/stdc++.h>

#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()

const char nl = '\n';
typedef long long ll;
typedef long double ld;

using namespace std;

const int inf = 1e9;

void solve() {
    vector<int> a;
    {
        int n;
        cin >> n;
        
        map<int, int> cnt;
        while (n--) {
            int x;
            cin >> x;
            cnt[x]++;
        }
        
        for (auto const &[k, v]: cnt) {
            a.push_back(v);
        }
    }
    
    int n = a.size();
    vector<int> dp(n + 1, inf);
    dp[0] = 0;
    
    for (int i = 1; i <= n; i++) {
        vector<int> ndp = dp;
        
        for (int k = 1; k <= n; k++) {
            int nv = dp[k - 1] + a[i - 1];
            
            if (nv <= i - k) {
                ndp[k] = min(ndp[k], nv);
            }
        }
        
        dp = ndp;
    }
    
    int ans = n;
    while (dp[ans] >= inf) ans--;
    cout << n - ans << nl;
}

int main() {
	ios::sync_with_stdio(0); cin.tie(0);
    
    int T;
    cin >> T;
    while (T--) solve();
}

• Good problem
• Average problem
• Bad problem

#include <bits/stdc++.h>

#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()

const char nl = '\n';
typedef long long ll;
typedef long double ld;

using namespace std;

const ll inf = 1e15;

void solve() {
    int n;
    cin >> n;
    
    vector<int> a(n);
    for (auto &x: a) cin >> x;
    
    vector<int> d(n);
    vector<vector<int>> g(n);
    for (int i = 1; i < n; i++) {
        int p;
        cin >> p;
        p--;
        
        g[p].push_back(i);
        d[i] = d[p] + 1;
    }
    
    vector<ll> b(n); // b[v] = sum(a[u]) - a[v]
    for (int v = 0; v < n; v++) {
        if (g[v].empty()) {
            b[v] = inf;
        } else {
            b[v] = -a[v];
        
            for (int u: g[v]) {
                b[v] += a[u];
            }
        }
    }
    
    ll ans = 0;
    for (int v = n - 1; v >= 0; v--) {
        queue<int> q;
        
        q.push(v);
        while (!q.empty()) {
            int i = q.front();
            q.pop();
            
            for (int u: g[i]) {
                ll delta = min(-b[v], b[u]);
                
                if (delta > 0) {
                    b[v] += delta;
                    b[u] -= delta;
                    ans += delta * (d[u] - d[v]);
                }
                
                q.push(u);
            }
        }
    }
    
    cout << ans << nl;
}

int main() {
	ios::sync_with_stdio(0); cin.tie(0);
    
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
}

• Good problem
• Average problem
• Bad problem

#include <bits/stdc++.h>

#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()

const char nl = '\n';
typedef long long ll;
typedef long double ld;

using namespace std;

const int inf = 1e9;

void solve() {
    int n;
    cin >> n;
    
    vector<int> a(n);
    for (int i = 0; i < n; i++) cin >> a[i];
    
    
    vector<vector<int>> dp(n + 1, vector<int> (n + 1, inf));
    
    for (int i = 0; i <= n; i++) {
        dp[i][i] = 0;
    }
    
    for (int le = 1; le <= n; le++) {
        for (int l = 0; l + le <= n; l++) {
            if (a[l] % 2 != (l + 1) % 2) continue;
            if (a[l] > l + 1) continue;
            int v = (l + 1 - a[l]) / 2;
            
            int r = l + le;
            for (int m = l + 1; m < r; m += 2) { // index of the closing bracket
                if (dp[l + 1][m] <= v) {
                    int new_val = max(v, dp[m + 1][r] - (m - l + 1) / 2);
                    dp[l][r] = min(dp[l][r], new_val);
                }
            }
        }
    }
    
    vector<int> dp2(n + 1);
    for (int i = 0; i < n; i++) {
        dp2[i + 1] = dp2[i];
        
        for (int j = 0; j < i; j++) {
            if (dp[j][i + 1] <= dp2[j]) {
                dp2[i + 1] = max(dp2[i + 1], dp2[j] + (i - j + 1) / 2);
            }
        }
    }
    
    cout << dp2[n] << nl;
}

int main() {
	ios::sync_with_stdio(0); cin.tie(0);
    
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
}

• Good problem
• Average problem
• Bad problem

• Good problem
• Average problem
• Bad problem

Consider that the edges are directed from $$$i \to l_i$$$ or $$$i \to r_i$$$ respectively. So that edges point from vertices with smaller values to vertices with larger values. That is $$$a \to b$$$ implies that $$$p_a < p_b$$$.

Notice that by definition, every vertex must have only $$$1$$$ edge that is going out of it. Therefore, if we consider the diameter to be something like $$$v_1 \to v_2 \to v_3 \to \ldots \to v_k \leftarrow \ldots \leftarrow v_{d-1} \leftarrow v_{d}$$$, since it is impossible for there to be some $$$\leftarrow v_i \to$$$ since each vertex has exactly one edge going out of it.

Therefore, it makes that we can split the path into 2 distinct parts: - $$$v_1 \to v_2 \to v_3 \to \ldots \to v_k$$$ - $$$v_d \to v_{d-1} \to \ldots \to v_{k}$$$

I claim that I can choose some $$$m$$$ such that the path $$$v_1 \to v_2 \to v_3 \to \ldots \to v_{k-1}$$$ and $$$v_d \to v_{d-1} \to \ldots \to v_{k+1}$$$ are in the range $$$[1,m]$$$ and $$$[m+1,n]$$$ or vice versa. That we are able to cut the array into half and each path will stay on their side.

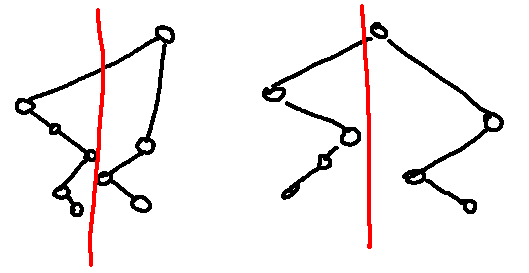
The red line shown above is the cutting line, as described. Proof is at the bottom under Proof 1 for completeness.

Now, we want to use this idea to make a meet in the middle solutions where we merge max stacks from both sides. Specifically: - maintain a max stack of elements as we are sweeping from $$$i=1\ldots n$$$. - for each element on the max stack, maintain the maximum size of a path that is rooted on that element.

Here is an example with $$$p=[4,1,5,3,2,6]$$$

• $$$i=1$$$: $$$s=[(4,1)]$$$
• $$$i=2$$$: $$$s=[(4,2),(1,1)]$$$
• $$$i=3$$$: $$$s=[(5,3)]$$$
• $$$i=4$$$: $$$s=[(5,3),(3,1)]$$$
• $$$i=5$$$: $$$s=[(5,3),(3,2),(2,1)]$$$
• $$$i=6$$$: $$$s=[(6,4)]$$$

When we insert a new element $$$x$$$, we pop all $$$(p_i,val)$$$ with $$$p_i < p_x$$$ and add in $$$(x,\max(val)+1)$$$ into the stack. Now, all elements of the stack has to updated with $$$s_{i,1} := \max(s_{i,1},s_{i+1,1}+1)$$$, which is really updating a suffix of $$$s_{*,1}$$$ with $$$val+k,\ldots,val+1,val$$$.

Firstly, it is clear that the $$$2$$$ vertices we merge, should have the biggest $$$p_i$$$ value, since a bigger $$$p_i$$$ value implies a bigger path size.

What we care about is the biggest path size possible only using vertices on $$$[1,i]$$$, which we denote array $$$best$$$. In the above example, $$$best = [1,2,3,3,4]$$$. We really only care about obtaining the array $$$best$$$ and not $$$s$$$. We can find this array in $$$O(n \log n)$$$ using segment trees or even in $$$O(n)$$$.

However, we cannot directly take the biggest values on each side. Consider $$$p=[2,1\mid,3,4]$$$. On the left and right side, the max stacks are $$$[2,1]$$$ and $$$[4,3]$$$ respectively, but we cannot connect $$$2$$$ with $$$4$$$ since the $$$3$$$ is blocking the $$$2$$$.

Suppose $$$a_1,a_2,\ldots,a_s$$$ are the prefix maximums while $$$b_1,b_2,\ldots,b_t$$$ are the suffix maximums.

Then, if the dividing line is at $$$a_i \leq m < a_{i+1}$$$, we will merge $$$a_i$$$ on the left side with $$$a_{i+1}$$$ on the right side. Similarly, if the dividing line is at $$$b_i \leq m < b_{i+1}$$$, we will merge $$$b_i$$$ on the left side with $$$b_{i+1}$$$ on the right side.

So, if $$$a_i \leq m < a_{i+1}$$$, it is equivalent to merging the best path on $$$[1,m]$$$ and $$$(m,a_{i+1})$$$ since then $$$a_{i+1}$$$ will be the root of the best path on the right side. It is similar for $$$b_i \leq m < b_{i+1}$$$.

Actually, we can prove that instead of $$$(m,a_{i+1})$$$, $$$(m,a_{i})$$$ is enough, and the proof is left as an exercise.

The total complexity becomes $$$O(n \log n)$$$ or $$$O(n)$$$ depending on how quickly array $$$best$$$ is found for subarrays.

Proof 1

Suppose that there are 2 paths $$$a_1 \to a_2 \to \ldots \to a_s$$$ and $$$b_1 \to b_2 \to \ldots \to b_t$$$, $$$a_1 < b_1$$$, and $$$a_s = b_t$$$ but they do not intersect at any vertices other vertices. Then we will prove that there is no such case where $$$a_s' > b_t'$$$.

Suppose that it is true that we can find some $$$a_{s'} > b_{t'}$$$.

#include <bits/stdc++.h>
using namespace std;

#define ii pair<int,int>
#define fi first
#define se second

#define pub push_back
#define pob pop_back

#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define sz(x) (int)(x).size()

int n;
int arr[400005];
string s;

int ans[2][400005];
int t[400005];
vector<int> stk[2];

vector<ii> process(int l,int r,int val[]){
	vector<ii> v;
	int curr=0;
	
	rep(x,l,r+1){
		ii res={x,0};
		while (!v.empty() && arr[v.back().fi]<arr[x]){
			int t=v.back().se; v.pob();
			if (!v.empty()) v.back().se=max(v.back().se,t+1);
			res.se=max(res.se,t+1);
		}
		v.pub(res);
		
		curr=max(curr,res.se+sz(v));
		val[x]=curr;
	}
	
	return v;
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin.exceptions(ios::badbit | ios::failbit);
	
	int TC;
	cin>>TC;
	while (TC--){
		cin>>n;
		rep(x,1,n+1) cin>>arr[x];
		cin>>s;
		
		rep(z,0,2){
			auto v=process(1,n,ans[z]);
			stk[z].clear();
			for (auto [a,b]:v) stk[z].pub(a);
			reverse(arr+1,arr+n+1);
		}
		
		int mx=ans[0][stk[0][0]]+ans[1][n-stk[0][0]+1]-1;
		
		rep(z,0,2){
			rep(x,0,sz(stk[z])-1){
				process(stk[z][x],stk[z][x+1],t);
				rep(y,stk[z][x],stk[z][x+1]) mx=max(mx,t[y]+ans[z^1][n-y]);
			}
			
			reverse(arr+1,arr+n+1);
		}
		
		cout<<mx-1<<endl;
	}
}

• Good problem
• Average problem
• Bad problem

#include <bits/stdc++.h>

#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()

const char nl = '\n';
typedef long long ll;
typedef long double ld;

using namespace std;

array<vector<int>, 2> get_l_and_r(vector<int> &p) {
    int n = p.size();
    
    vector<int> l(n), r(n);
    
    stack<int> s;
    for (int i = 0; i < n; i++) {
        while (!s.empty() && p[s.top()] < p[i]) s.pop();
        
        if (s.empty()) l[i] = -1;
        else l[i] = s.top();
        
        s.push(i);
    }
    
    s = {};
    for (int i = n - 1; i >= 0; i--) {
        while (!s.empty() && p[s.top()] < p[i]) s.pop();
        
        if (s.empty()) r[i] = n;
        else r[i] = s.top();
        
        s.push(i);
    }
    
    return {l, r};
}

int ans_l_edge(array<int, 2> d, array<int, 2> e) {
    return d[0] + 1 + max(d[1], e[0]);
}

int ans_r_edge(array<int, 2> d, array<int, 2> e) {
    return e[1] + 1 + max(d[1], e[0]);
}

array<int, 2> add_l_edge(array<int, 2> d, array<int, 2> e) {
    return {max({d[0], d[1] + 1, e[0] + 1}), e[1]};
}

array<int, 2> add_r_edge(array<int, 2> d, array<int, 2> e) {
    return {d[0], max({d[1] + 1, e[0] + 1, e[1]})};
}

vector<array<int, 2>> process_dp(vector<array<int, 2>> &dp) {
    array<int, 2> max_a = {-1, -1}, max_b = {-1, -1}, max_s = {-1, -1};
    
    for (auto [a, b]: dp) {
        if (a > max_a[0] || (a == max_a[0] && b > max_a[1])) {
            max_a = {a, b};
        }
        
        if (b > max_b[1] || (b == max_b[1] && a > max_b[0])) {
            max_b = {a, b};
        }
        
        if (a + b > max_s[0] + max_s[1]) {
            max_s = {a, b};
        }
    }
    
    return {max_a, max_b, max_s};
}

void add_to_map(map<array<int, 2>, int> &dp_ind, int &len_dp, array<int, 2> a) {
    if (!dp_ind.count(a)) {
        dp_ind[a] = len_dp++;
    }
}

void solve() {
    int n;
    cin >> n;
    
    vector<int> p(n);
    for (int i = 0; i < n; i++) cin >> p[i];
    
    string s;
    cin >> s;
    
    auto [l, r] = get_l_and_r(p);
    
    for (int i = 0; i < n; i++) {
        if (p[i] == n) continue;
        
        if (l[i] == -1 && s[i] == 'L') {
            cout << -1 << nl;
            return;
        }
        
        if (r[i] == n && s[i] == 'R') {
            cout << -1 << nl;
            return;
        }
    }
    
    int ans = 0;
    
    vector<int> q(n + 1);
    for (int i = 0; i < n; i++) {
        q[p[i]] = i;
    }
    
    int len_dp = 0;
    map<array<int, 2>, int> dp_ind;
    
    for (int x = 1; x <= n; x++) {
        int i = q[x];
        int tl = l[i], tr = r[i];
        
        add_to_map(dp_ind, len_dp, {tl, i});
        add_to_map(dp_ind, len_dp, {i, tr});
        add_to_map(dp_ind, len_dp, {tl, tr});
    }
    
    vector<vector<array<int, 2>>> dp(len_dp, {{0, 0}});
    for (int x = 1; x <= n; x++) {
        int i = q[x];
        int tl = l[i], tr = r[i];
        
        int ind_l = dp_ind[{tl, i}];
        int ind_r = dp_ind[{i, tr}];
        int ind_c = dp_ind[{tl, tr}];
        
        for (auto const &d: dp[ind_l]) {
            for (auto const &e: dp[ind_r]) {
                ans = max(ans, d[1] + e[0]);
                
                if (tl >= 0 && s[i] != 'R') {
                    ans = max(ans, ans_l_edge(d, e));
                    dp[ind_c].push_back(add_l_edge(d, e));
                }
                
                if (tr <= n - 1 && s[i] != 'L') {
                    ans = max(ans, ans_r_edge(d, e));
                    dp[ind_c].push_back(add_r_edge(d, e));
                }
            }
        }
        
        dp[ind_c] = process_dp(dp[ind_c]);
    }
    
    cout << ans << nl;
}

int main() {
	ios::sync_with_stdio(0); cin.tie(0);

    int T;
    cin >> T;
    while (T--) {
        solve();
    }
}

• Good problem
• Average problem
• Bad problem

#include <bits/stdc++.h>

#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()

const char nl = '\n';
typedef long long ll;
typedef long double ld;

using namespace std;

int ans_x = 0, ans_y = 0, cnt_q = 0;
// Coordinates are flipped
int query(int x, int y) {
    cnt_q++;

    int res = 0;
    cout << "? " << y << ' ' << x << endl;
    cout.flush();
    
    cin >> res;
    
    if (res < 0) {
        exit(0);
    }
    
    if (res == 0) {
        ans_x = x;
        ans_y = y;
    }
    
    return res;
}

/* Explanation:
 * Splits the stripe of three into |a-O-a-b-O-b-a-O-a|.
 * O are the three query points (all in the same column). 
 * Cons: hard to correctly account for errors in a non-bruteforce way.
 * Pros: gives a better constant factor (3 / 4 of the original length)
 * Number of queries: n + 3 * 21 + 25 * ceil(log(25, 2)) + eps 
 * Though the binary search part uses less queries than that */

void f(int lx, int rx, int ly, int ry) {
    int n = rx - lx + 1;
    
    // Bruteforce base case (uses binary search)
    if (n <= 25) { // can be n <= 22 or above
        for (int x = lx; x <= rx; x++) {
            int lb = ly, ub = ry;
            
            while (lb <= ub) {
                int res = query(x, lb);
                
                int low_y = ((res - 1) + 1) / 2, high_y = res;
                
                int new_lb = lb + max(1, low_y), new_ub = min(ub, lb + high_y);
                lb = new_lb;
                ub = new_ub;
            }
        }
        
        return;
    }
    
    
    // Here, (2a - 1) + (2b - 1) + (2a - 1) = n
    int a = 3 * (n + 3) / 16;
    int y = min(ry, ly + 1);
    
    int x1 = lx + a - 1;
    x1 = max(x1, lx);
    x1 = min(x1, rx);
    
    int x2 = (lx + rx) / 2;
    x2 = max(x2, x1 + 1);
    x2 = min(x2, rx);
    
    int x3 = rx - a + 1;
    x3 = max(x3, x2 + 1);
    x3 = min(x3, rx);


    int m = min(3, ry - ly + 1);
    vector<vector<bool>> good(n, vector<bool> (m, true));
    
    int new_lx = lx, new_rx = rx;
    int new_ly = ly, new_ry = ry;
    
    for (int x: {x1, x2, x3}) {
        int res = query(x, y);
        
        new_lx = max(new_lx, x - res);
        new_rx = min(new_rx, x + res);
        
        new_ly = max(new_ly, y - res);
        new_ry = min(new_ry, y + res);
        
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                int r_x = lx + i, r_y = ly + j;
                
                int dx = abs(r_x - x);
                int dy = abs(r_y - y);
                
                int d = dx + dy;
                int S = (dx + 1) * (dy + 1);
                
                // d <= res <= d + S must hold
                if (res < d || d + S < res) {
                    good[i][j] = false;
                }
            }
        }
    }
    
    bool has_good = false;
    for (auto vx: good) {
        for (auto vy: vx) {
            if (vy) {
                has_good = true;
            }
        }
    }
    good.clear();
    good.shrink_to_fit();
    
    if (has_good) {
        f(new_lx, new_rx, new_ly, new_ry);
    } else {
        f(lx, rx, ly + m, ry);
    }
}

void solve() {
    int n, m;
    cin >> n >> m;
    ans_x = 0; ans_y = 0; cnt_q = 0;
    
    f(1, m, 1, n);
    
    cout << "! " << ans_y << ' ' << ans_x << endl;
    cout.flush();
    
    cerr << n << ' ' << cnt_q << " | " << n + 225 << endl;
}

int main() {
	ios::sync_with_stdio(0); cin.tie(0);
    
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
}

• Good problem
• Average problem
• Bad problem