Given $$$N$$$ integer intervals $$$[a, b]$$$, find the maximum number of pairs of overlapping intervals where each interval can belong to at most one pair.
Two intervals overlap if they share a common point, including closed endpoints.
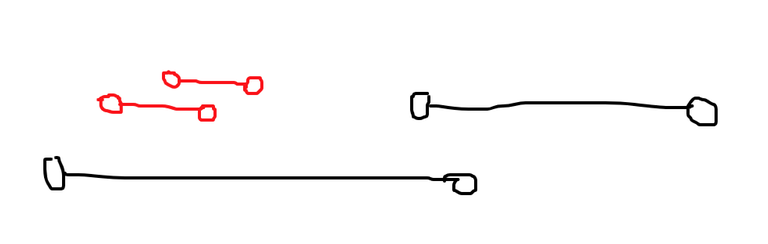
The answer to the example above is 2. Pair the 2 black intervals and the 2 red intervals together.
What is the best time complexity that can be achieved for this problem? Currently I'm not sure if it's even solvable in polynomial time.





