First,it's not hard to come up with query $$$? 1$$$.Assume we have got $$$t$$$,the answer is either $$$2t$$$ or $$$2t-1$$$.
Then we can query $$$? 2t$$$.It can be proven the answer of $$$? 2t$$$ is always different from $$$? 2t$$$.
Another approach:query $$$? 2$$$ or $$$? 2m-1$$$.Although it doesn't work in some small cases,you can do another query to avoid confilct.
104855B - Yugandhar's Letter for Diya
Every time choosing adjacent cell to blue cell is optimal because it can stop the growth of blue cell in that particular direction, so obviously if k>=4 we can surround the blue cell so answer will be nm-1.
For k=1 we will take the portion (up side, down side, left side, right side) of cells to initial blue cell containing maximum white cells, similarly for k=2 (2 portions) and 3 (3 portions).
In general, the score for index $$$i$$$ is:
$$$\Sigma_{j = 1}^{i} min(a_j, a_i)$$$ + $$$\Sigma_{j = i + 1}^{n} min(a_j, a_i - 1)$$$
Let's solve this problem starting from the box which has the smallest number of salmons, until the largest number of salmons. This can be calculated by some simple algebra with the help of data structure such as fenwick tree.
Let's maintain the set of \textit{reachable} nodes (i.e. nodes $$$x$$$ such that there exist a \textit{colorful} path starting from $$$1$$$ and ending at $$$x$$$)~--- $$$Q$$$, alongside with the set of colors we can reach node $$$v$$$ with (i.e. the set of distinct colors of last edge of all valid \textit{colorful} paths starting from $$$1$$$ and ending at $$$v$$$)~--- $$$colors[v]$$$ for each $$$v$$$.
Now, we will process nodes, one by one, in bfs order using queue $$$Q$$$.
Let $$$v$$$ be the node we currently processing. Since $$$v \in Q$$$ then $$$colors[v]$$$ is non-empty.
Let's notice that in the case of having at least $$$2$$$ distinct colors in the $$$colors[v]$$$, we can extend the current \textit{colorful} path with outgoing edges from $$$v$$$ of any color, while in case of $$$color[v]$$$ containing a single color~--- $$$c$$$, we can extend the current \textit{colorful} path with outgoing edges from $$$v$$$ of any color, except for $$$c$$$.
Clearly, we only need to maintain at most $$$2$$$ colors in $$$colors[v]$$$. Moreover, we will add node $$$v$$$ in $$$Q$$$ only when the size of $$$color[v]$$$ is changed.
Therefore, we will process each node at most $$$2$$$ times, so the total complexity will be $$$O(n + m)$$$.
Let's consider what's the possible value set.
Let's write $$$a_1+b_2+a_3+c_4+\dots$$$ like a string \t{abac...}
We can achieve the string iff:
\begin{itemize} \item When we remove all \t{b}, the remaining string begins with \t{c} and ends with \t{a}. \end{itemize}
Necessity is almost obvious.
Then, how to construct? Let's think about an example : \t{bbccbabaabbcba}.
First, when $$$S_i=b$$$, let's set $$$p_i = i$$$. Now $$$p=(1,2,?,?,5,?,7,?,?,10,11,?,13,?)$$$.
Next, split the remaining string(consist of only \t{a} or \t{c}) into \t{cc...caa...a}.
Finally, we can achieve every \t{cc...caa...a} with a rotation of $$$p_i = i$$$.
Let's consider $$$3,4,6,8,9$$$-th characters. They are \t{ccaaa}. Then, we rotate $$$p$$$ to $$$(8,9,3,4,6)$$$ and back them to original place.
In this example, possible final $$$p=(1,2,8,9,5,3,7,4,6,10,11,14,13,12)$$$.
Now only we should do is restoreing the string. It's possible to do a DP with following states:
\begin{itemize} \item There are no \t{a} and \t{c}. \item When we remove all \t{b}, current string ends with \t{c}. \item When we remove all \t{b}, current string ends with \t{a}. \end{itemize}
For the first test case, the points and the polygon looks like this:
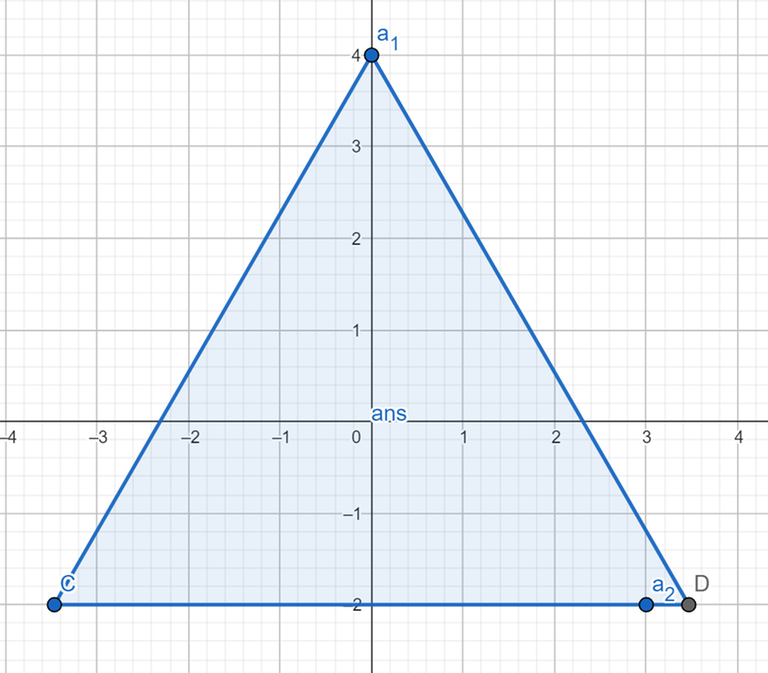
If the size of the polygon is less than $$$4$$$, the point $$$a_1$$$ cannot be covered by the polygon no matter how the polygon is placed. Thus, the minimum size of the polygon is $$$4$$$.
For the second test case, the points and the polygon looks like this:
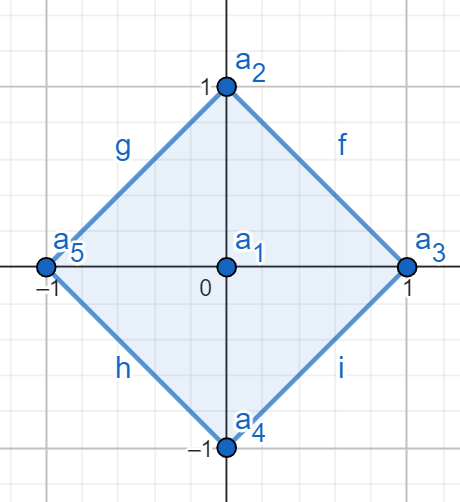
#include <map>
#include <set>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <cstdio>
#include <cstdlib>
#include <vector>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
typedef double db;
typedef long long ll;
typedef unsigned long long ull;
const int N=1000010;
const int LOGN=28;
const ll TMD=0;
const ll INF=2147483647;
int T,t,tt;
int main()
{
//freopen("test.in","r",stdin);
scanf("%d",&T);
while(T--)
{
printf("? 1\n");
fflush(stdout);
scanf("%d",&t);
printf("? %d\n",t*2);
fflush(stdout);
scanf("%d",&tt);
printf("! %d\n",t*2-(tt!=t*2));
fflush(stdout);
}
//fclose(stdin);
return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define fast \
ios_base::sync_with_stdio(0); \
cin.tie(0); \
cout.tie(0);
int main(){
fast;
ll t;
cin>>t;
while(t--){
ll n,m,x,y,k;
cin>>n>>m>>x>>y>>k;
ll a1=(n*m)-(n*y);
ll a2=(n*m)-(m*x);
ll a3=(n*m)-(n*(m-y+1));
ll a4=(n*m)-(m*(n-x+1));
if(k==0) cout<<0<<endl;
else if(k==1) cout<<max({a1,a2,a3,a4})<<endl;
else if(k==2){
ll b1=a1+max((n-x)*y,(x-1)*y);
ll b2=a2+max(x*(y-1),x*(m-y));
ll b3=a3+max((m-y+1)*(x-1),(m-y+1)*(n-x));
ll b4=a4+max((n-x+1)*(m-y),(n-x+1)*(y-1));
ll b5=a1+a3;
ll b6=a2+a4;
cout<<max({b1,b2,b3,b4,b5,b6})<<endl;
}
else if(k==3){
a1=n-x;
a2=x-1;
a3=m-y;
a4=y-1;
cout<<n*m-1-min({a1,a2,a3,a4})<<endl;
}
else cout<<(n*m-1)<<endl;
}
}
#include <bits/stdc++.h>
#define int long long
#define fi first
#define se second
using namespace std;
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while (t --> 0) {
int n;
cin >> n;
map<int, int> cnt;
vector<pair<int, int>> a;
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
cnt[x] += 1;
a.push_back({x, i});
}
sort(a.begin(), a.end(), [&](pair<int, int> x, pair<int, int> y) {
if (x.fi != y.fi) return x.fi < y.fi;
return x.se > y.se;
});
vector<int> fen(n + 1);
auto upd = [&](int x, int val) {
for (; x <= n; x += x & -x) fen[x] += val;
};
auto get = [&](int x) {
int res = 0;
for (; x > 0; x -= x & -x) res += fen[x];
return res;
};
for (int i = 1; i <= n; i++) upd(i, 1);
int lst = 0, cur = 0;
vector<int> ans(n + 1);
for (int p = 0; p < n; p++) {
auto [x, i] = a[p];
if (p == 0) {
cur += (x - 1) * n;
lst = x - 1;
} else if (a[p - 1].fi != x) {
cur += (x - lst - 1) * get(n);
cur += cnt[lst + 1];
lst = x - 1;
}
ans[i] = cur + get(i);
upd(i, -1);
}
for (int i = 1; i <= n; i++) cout << ans[i] << " \n"[i == n];
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n, m;
cin >> n >> m;
vector<vector<pair<int, int>>> g(n);
for (int i = 0; i < m; ++i) {
int u, v, c;
cin >> u >> v >> c;
--u; --v; --c;
g[u].push_back({v, c});
}
vector<int> ans(n);
vector<vector<int>> colors(n);
colors[0].push_back(-1);
colors[0].push_back(-1);
vector<int> Q;
Q.push_back(0);
while (!Q.empty()) {
int u = Q.back();
Q.pop_back();
ans[u] = true;
if (colors[u].size() == 2) {
for (auto el : g[u]) {
int v = el.first;
int c = el.second;
if (colors[v].size() == 2) {
continue;
}
if (colors[v].empty()) {
colors[v].push_back(c);
Q.push_back(v);
continue;
}
if (colors[v][0] != c) {
colors[v].push_back(c);
Q.push_back(v);
}
}
} else if (colors[u].size() == 1) {
int cur = colors[u][0];
for (auto el : g[u]) {
int v = el.first;
int c = el.second;
if (c == cur) {
continue;
}
if (colors[v].size() == 2) {
continue;
}
if (colors[v].empty()) {
colors[v].push_back(c);
Q.push_back(v);
continue;
}
if (colors[v][0] != c) {
colors[v].push_back(c);
Q.push_back(v);
}
}
}
}
for (int i = 0; i < n; ++i) {
if (ans[i]) {
cout << i + 1 << " ";
}
}
cout << "\n";
}
int32_t main() {
cin.tie(0);
ios_base::sync_with_stdio(false);
int t;
cin >> t;
for (int _ = 0; _ < t; ++_) {
solve();
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
using pi=pair<int,int>;
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while(t>0){
t--;
int n;
cin >> n;
vector<int> a(n);
for(auto &nx : a){cin >> nx;}
vector<int> b(n);
for(auto &nx : b){cin >> nx;}
vector<int> c(n);
for(auto &nx : c){cin >> nx;}
// 0 ... nothing
// 1 ... cc...caa...acc...
// 2 ... cc...caa...a
vector<vector<long long>> dp(n,vector<long long>(3,-8e18));
vector<vector<pi>> pre(n,vector<pi>(3));
dp[0][0]=b[0];
pre[0][0]={-1,1};
dp[0][1]=c[0];
pre[0][1]={-1,2};
for(int i=1;i<n;i++){
// from 0
if(dp[i][0] < dp[i-1][0]+b[i]){
dp[i][0]=dp[i-1][0]+b[i];
pre[i][0]={0,1};
}
if(dp[i][1] < dp[i-1][0]+c[i]){
dp[i][1]=dp[i-1][0]+c[i];
pre[i][1]={0,2};
}
// from 1
if(dp[i][2] < dp[i-1][1]+a[i]){
dp[i][2]=dp[i-1][1]+a[i];
pre[i][2]={1,0};
}
if(dp[i][1] < dp[i-1][1]+b[i]){
dp[i][1]=dp[i-1][1]+b[i];
pre[i][1]={1,1};
}
if(dp[i][1] < dp[i-1][1]+c[i]){
dp[i][1]=dp[i-1][1]+c[i];
pre[i][1]={1,2};
}
// from 2
if(dp[i][2] < dp[i-1][2]+a[i]){
dp[i][2]=dp[i-1][2]+a[i];
pre[i][2]={2,0};
}
if(dp[i][2] < dp[i-1][2]+b[i]){
dp[i][2]=dp[i-1][2]+b[i];
pre[i][2]={2,1};
}
if(dp[i][1] < dp[i-1][2]+c[i]){
dp[i][1]=dp[i-1][2]+c[i];
pre[i][1]={2,2};
}
}
// for(auto &nx : dp){
// for(auto &ny : nx){cout << ny << " ";}
// cout << "\n";
// }
vector<int> pt;
int tg;
if(dp[n-1][0]<dp[n-1][2]){tg=2;}else{tg=0;}
// cout << max(dp[n-1][0],dp[n-1][2]) << "\n";
vector<int> his(n);
for(int i=n-1;i>=0;i--){
his[i]=pre[i][tg].second;
tg=pre[i][tg].first;
}
vector<int> p(n);
int ofs=0;
vector<int> sft;
// for(auto &nx : his){cout << nx << " ";}cout << "\n";
his.push_back(2);
int phs=0;
for(int i=0;i<=n;i++){
if(his[i]==2){
if(phs==2){
int sz=sft.size();
for(int i=0;i<sz;i++){
p[sft[(i+ofs)%sz]]=sft[i];
}
ofs=0;
sft.clear();
}
sft.push_back(i);
ofs++;
phs=1;
}
else if(his[i]==1){p[i]=i;}
else if(his[i]==0){
if(phs==1){phs=2;}
sft.push_back(i);
}
}
long long act=0;
for(int i=0;i<n;i++){
if(p[i]<i){act+=a[i];}
else if(p[i]==i){act+=b[i];}
else{act+=c[i];}
}
// cout << act << "\n";
for(int i=0;i<n;i++){
if(i){cout << " ";}
cout << p[i]+1;
}cout << "\n";
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
const long double PI=acosl(-1);
const int MAXN=2e5+2;
pair<long double,long double> xy[MAXN];
vector<pair<long double,bool>> sweep;
int main() {
int t;
cin >> t;
while (t--) {
int n,m;
cin >> n >> m;
long double x,y,ang,rot=2*PI/m,maxDist=0;
for (int i=1;i<=n;i++) {
cin >> x >> y;
ang=atan2l(y,x);
ang-=floorl(ang/rot)*rot;
xy[i]={sqrtl(x*x+y*y),ang};
maxDist=max(maxDist,xy[i].first);
}
long double l=maxDist,r=3*maxDist,mid;
int cnt,cnt2;
while (r-l >= 1e-10) {
cnt=0;cnt2=0;sweep.clear();
mid=(l+r)/2; // bin search on size
for (int i=1;i<=n;i++) {
if (xy[i].first <= mid*cosl(rot/2)) continue;
cnt++;
ang=rot/2-acosl(mid*cosl(rot/2)/xy[i].first);
if (xy[i].second < ang) {
sweep.push_back({rot+xy[i].second-ang,0});
sweep.push_back({ang+xy[i].second,1});
sweep.push_back({0,0});
}
else if (xy[i].second >= rot-ang) {
sweep.push_back({0,0});
sweep.push_back({ang-rot+xy[i].second,1});
sweep.push_back({xy[i].second-ang,0});
}
else {
sweep.push_back({ang+xy[i].second,1});
sweep.push_back({xy[i].second-ang,0});
}
}
sort(sweep.begin(),sweep.end());
for (auto &i : sweep) {
if (i.second) cnt2--;
else cnt2++;
if (cnt2 == cnt) break;
}
if (cnt2 != cnt) l=mid;
else r=mid;
}
cout << setprecision(10) << l << endl;
}
}





