IOI 2023 Robot Contest in Z* = 5

№	Пользователь	Рейтинг
1	tourist	3993
2	jiangly	3743
3	orzdevinwang	3707
4	Radewoosh	3627
5	jqdai0815	3620
6	Benq	3564
7	Kevin114514	3443
8	ksun48	3434
9	Rewinding	3397
10	Um_nik	3396

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	155
8	TheScrasse	154
9	Dominater069	153
10	nor	152

IOI 2023 Robot Contest is a great task that reminds me of Turing machines and cellular automata.

If the task statement is too intimidating...

The model solution is in $$$Z^\star = 6$$$. Let's do it in $$$Z^\star = 5$$$!

Besides color $$$0$$$ ("blank") and color $$$1$$$ ("path"), colors $$$2,3,4,5$$$ will represent the cardinal directions. Call them "arrows".

In the first phase, we run a BFS which works as follows:

Invariant: The graph formed by following the arrows forms a tree that converges to two arrows pointing to each other, with Pulibot on one of these two arrows, or to a blank cell, with Pulibot on said cell.
To begin this phase, we have the special case that, if Pulibot is on a blank cell and there is out-of-bounds to the west and north of Pulibot, it will change its cell to a south arrow and move south, unless there is an obstacle there, in which case it will do the same thing but with east. (We make the first move immediately to avoid ambiguities with the second phase.)
If Pulibot is on an arrow, it rotates said arrow counterclockwise (a nonzero amount) until it points to either a blank cell or an arrow that points back. It then moves to this cell.
If Pulibot is on a blank cell, it finds the unique arrow pointing to it and moves to it, changing the current cell to an arrow pointing in the direction it moved.

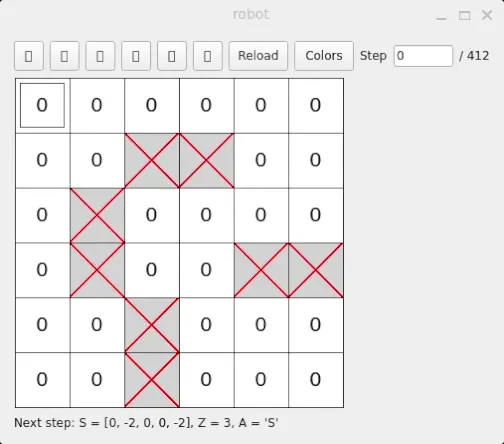
This procedure traverses the tree and expands it one node whenever Pulibot encounters a blank cell. By transitioning based on rotating arrows, we guarantee that we visit each branch of the tree exactly once each traversal, so this is a BFS and the path along the tree between the corners is a shortest path. A fun fact, if we view the edge formed by the two arrows pointing to each other as being "selected", this is an Euler tour!

Once we reach the southeast corner, we begin the second phase, which deletes the tree and leaves behind the path.

Invariant: The graph formed by following the arrows forms a tree that points to east of the northeast corner, with Pulibot on any arrow. This lets Pulibot figure out that it is in the second phase by noticing that it is not on an empty cell and its cell points to a cell that is not an arrow pointing back.
To begin this phase, we have the special case that, if Pulibot is on a blank cell and there is out-of-bounds to the east and south of Pulibot, it will change its cell to an east arrow and stay in place.
If an arrow points to Pulibot's cell, it moves to it (not changing the cell it is on). If there are multiple such arrows, choosing any works.
If no arrow points to Pulibot's cell, it moves to where its cell is pointing, unless it is already at the southeast corner, in which case it terminates. It replaces its cell with path if it is at the northwest corner or there is path adjacent to it, and with blank otherwise.

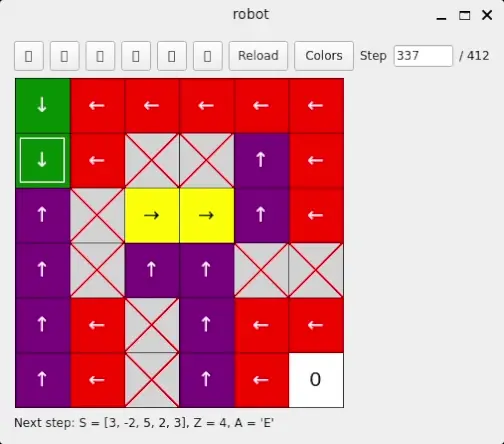
This phase runs a DFS that deletes (but doesn't modify) the tree by "falling" down to the leaves and "pulling" them up. The path between the corners will clearly be replaced with path, but what about other nodes? Since this tree is a BFS tree when rooted at the northwest corner, for every cell not on the shortest path that is adjacent to the shortest path, following arrows until reaching the shortest path must lead to a shortest path cell no farther from the northwest corner than the shortest path cell adjacent to the cell (otherwise connecting the cell to the adjacent shortest path cell would be a shorter path to the northwest corner). Since the tree is deleted depth-first when rooted at the southeast corner, it will be deleted before the adjacent shortest path cell becomes path.

And that's it! The task's API requires you to set the move for each specific set of colors, but it's much easier to write a function that calculates the move given the set of colors and loop over all possibilities.

Code

#include "robot.h"
#include <bits/stdc++.h>

using namespace std;

enum Id {
    Bound = -2,
    Block,
    Empty,
    Path,
    West,
    South,
    East,
    North,
    Imp,
};
array<char,4> dirs{{'W','S','E','N'}};
pair<int,char> IMP = {Imp,'T'};

pair<int,char> move(array<int,5> S) {
    auto [h,w,s,e,n] = S;
    if (h == Empty) {
        if (w == Bound && n == Bound) {
            // start BFS phase
            if (s == Empty) {
                return {South,'S'};
            } else {
                return {East,'E'};
            }
        } else if (e == Bound && s == Bound) {
            // start pruning phase
            return {East,'H'};
        } else {
            // extend tree
            for (int i = 0; i < 4; ++i) {
                if (S[i+1]-West == (i+2)%4) return {West+i,dirs[i]};
            }
            return IMP;
        }
    } else if (0 <= h-West && h-West < 4) {
        int dir = h-West;
        if (S[dir+1]-West == (dir+2)%4) {
            // traverse tree
            int i = dir;
            do {
                i = (i+1)%4;
                if (S[i+1]-West == (i+2)%4 || S[i+1] == Empty) return {West+i,dirs[i]};
            } while (i != dir);
            return IMP;
        } else {
            // pruning phase
            int i = dir;
            bool path = false;
            do {
                i = (i+1)%4;
                // traverse to tile other than previous
                if (S[i+1]-West == (i+2)%4) return {h,dirs[i]};
                if (S[i+1] == Path) path = true;
            } while (i != dir);
            // prune
            return {
                path || (w == Bound && n == Bound) ? Path : Empty,
                e == Bound && s == Bound ? 'T' : dirs[i],
            };
        }
    } else {
        return IMP;
    }
}

#define FR(x) for (int x = Bound; x < Imp; ++x)

void program_pulibot()
{
    FR(h) FR(w) FR(s) FR(e) FR(n) {
        auto [Z,A] = move({h,w,s,e,n});
        if (Z > 5) continue;
        set_instruction({h,w,s,e,n}, Z, A);
    }
}

The code was tested on oj.uz.

Some background for what led to this

In-contest, I was able to come up with the BFS phase pretty quickly, but then I got stuck for over 2 hours on how to construct the path from the BFS tree. I couldn't figure out how to make sure the bot "remembers" it is now in the second phase, not realizing that I could break the two-arrows-pointing-to-each-other invariant.

Also, I set all the instructions manually, using only a helper that let me pass in bit fields for multiple colors. As a result, the code was horrible and also I rotated one quarter turn at a time, which weakens the invariant. In the end I added 4 additional states, also representing the cardinal directions but with the information that this is the second stage. Upon reaching the southeast corner, Pulibot converts the old arrows to these new arrows and it deletes the tree similarly.

After the contest, during the analysis time (when we're allowed back to the computers to test and submit appeals if necessary), a committee member came up to me to tell me they came up with a $$$Z^\star = 5$$$ solution based on my solution, which they didn't know was possible before. Unfortunately they said it probably wouldn't be shared, but they left the hint that it was the same up until Pulibot reaches the southeast corner.

My (very bad) in-contest code

#include "robot.h"
#include <bits/stdc++.h>

using namespace std;

enum Stat {
    BOUND = 1,
    BLOCK = 2,
    EMPTY = 4,
    PATH = 8,
    BRIGHT = 16,
    UP = 32,
    DOWN = 64,
    LEFT = 128,
    RIGHT = 256,
    BUP = 512,
    BDOWN = 1024,
    BLEFT = 2048,
    // special
    ANY = 4095,
    ANP = ANY & ~(EMPTY | PATH | BUP | BDOWN | BLEFT | BRIGHT),
    BAD = BOUND | BLOCK,
    INIT = BAD | EMPTY,
};

enum Col {
    Bound = -2,
    Block,
    Empty,
    Path,
    BRight,
    Up,
    Down,
    Left,
    Right,
    BUp,
    BDown,
    BLeft,
};
#define OPEN(v,i)\
    for (int v = -2; v <= 10; ++v) {\
        if (!((S[i]>>(v+2))&1)) continue;
#define CLOS(v,i)\
    }
set<array<int,5>> seen;
void si(array<int,5> S, Col Z, char A, bool exc = false) {
    OPEN(a,0)
    OPEN(b,1)
    OPEN(c,2)
    OPEN(d,3)
    OPEN(e,4)
    if (exc && c == Bound && d == Bound) continue;
    if (seen.count({a,b,c,d,e})) continue;
    set_instruction({a,b,c,d,e},Z,A);
    seen.insert({a,b,c,d,e});
    CLOS(e,4)
    CLOS(d,3)
    CLOS(c,2)
    CLOS(b,1)
    CLOS(a,0)
}

void program_pulibot()
{
    // init
    si({EMPTY,BOUND,INIT,INIT,BOUND},Left,'H',true);
    // cont
    si({LEFT,ANP,ANY&~(EMPTY|UP),ANY,ANY},Down,'H');
    si({DOWN,ANY,ANP,ANY&~(EMPTY|LEFT),ANY},Right,'H');
    si({RIGHT,ANY,ANY,ANP,ANY&~(EMPTY|DOWN)},Up,'H');
    si({UP,ANY&~(EMPTY|RIGHT),ANY,ANY,ANP},Left,'H');
    // traverse
    si({LEFT,ANP,UP,ANY,ANY},Down,'S');
    si({DOWN,ANY,ANP,LEFT,ANY},Right,'E');
    si({RIGHT,ANY,ANY,ANP,DOWN},Up,'N');
    si({UP,RIGHT,ANY,ANY,ANP},Left,'W');
    // explore
    si({LEFT,ANP,EMPTY,ANY,ANY},Down,'S');
    si({DOWN,ANY,ANP,EMPTY,ANY},Right,'E');
    si({RIGHT,ANY,ANY,ANP,EMPTY},Up,'N');
    si({UP,EMPTY,ANY,ANY,ANP},Left,'W');
    // new
    si({EMPTY,ANY&~RIGHT,ANY&~UP,ANY&~LEFT,DOWN},Up,'N',true);
    si({EMPTY,RIGHT,ANY&~UP,ANY&~LEFT,ANY&~DOWN},Left,'W',true);
    si({EMPTY,ANY&~RIGHT,UP,ANY&~LEFT,ANY&~DOWN},Down,'S',true);
    si({EMPTY,ANY&~RIGHT,ANY&~UP,LEFT,ANY&~DOWN},Right,'E',true);
    // found
    si({EMPTY,ANY,BOUND,BOUND,ANY},BUp,'H');
    // done
    si({ANY,PATH,BOUND,BOUND,ANY},Path,'T');
    si({ANY,ANY,BOUND,BOUND,PATH},Path,'T');
    // cont
    si({BLEFT,ANY,ANY&~(UP|BUP),ANY,ANY},BDown,'H');
    si({BDOWN,ANY,ANY,ANY&~(LEFT|BLEFT),ANY},BRight,'H');
    si({BRIGHT,ANY,ANY,ANY,ANY&~(DOWN|BDOWN)},BUp,'H');
    si({BUP,ANY&~(RIGHT|BRIGHT),ANY,ANY,ANY},BLeft,'H');
    // trash path init
    si({BLEFT,BOUND,BUP,ANY&~BLEFT,BOUND},Path,'S');
    si({BDOWN,BOUND,ANY&~BUP,BLEFT,BOUND},Path,'E');
    // trash path
    si({BLEFT,PATH,BUP,ANY&~BLEFT,ANY&~BDOWN},Path,'S');
    si({BLEFT,ANY&~BRIGHT,BUP,PATH,ANY&~BDOWN},Path,'S');
    si({BLEFT,ANY&~BRIGHT,BUP,ANY&~BLEFT,PATH},Path,'S');
    si({BDOWN,PATH,ANY&~BUP,BLEFT,ANY&~BDOWN},Path,'E');
    si({BDOWN,ANY&~BRIGHT,PATH,BLEFT,ANY&~BDOWN},Path,'E');
    si({BDOWN,ANY&~BRIGHT,ANY&~BUP,BLEFT,PATH},Path,'E');
    si({BRIGHT,PATH,ANY&~BUP,ANY&~BLEFT,BDOWN},Path,'N');
    si({BRIGHT,ANY&~BRIGHT,PATH,ANY&~BLEFT,BDOWN},Path,'N');
    si({BRIGHT,ANY&~BRIGHT,ANY&~BUP,PATH,BDOWN},Path,'N');
    si({BUP,BRIGHT,PATH,ANY&~BLEFT,ANY&~BDOWN},Path,'W');
    si({BUP,BRIGHT,ANY&~BUP,PATH,ANY&~BDOWN},Path,'W');
    si({BUP,BRIGHT,ANY&~BUP,ANY&~BLEFT,PATH},Path,'W');
    // trash empty
    si({BLEFT,ANY&~BRIGHT,BUP,ANY&~BLEFT,ANY&~BDOWN},Empty,'S');
    si({BDOWN,ANY&~BRIGHT,ANY&~BUP,BLEFT,ANY&~BDOWN},Empty,'E');
    si({BRIGHT,ANY&~BRIGHT,ANY&~BUP,ANY&~BLEFT,BDOWN},Empty,'N');
    si({BUP,BRIGHT,ANY&~BUP,ANY&~BLEFT,ANY&~BDOWN},Empty,'W');
    // travs
    si({BUP,BRIGHT,BUP,ANY,ANY},BLeft,'W');
    si({BUP,BRIGHT,ANY&~BUP,BLEFT,ANY},BLeft,'W');
    si({BUP,BRIGHT,ANY&~BUP,ANY&~BLEFT,BDOWN},BLeft,'W');
    si({BLEFT,ANY&~BRIGHT,BUP,BLEFT,ANY},BDown,'S');
    si({BLEFT,ANY&~BRIGHT,BUP,ANY&~BLEFT,BDOWN},BDown,'S');
    si({BDOWN,ANY&~BRIGHT,ANY&~BUP,BLEFT,BDOWN},BRight,'E');
    // trav fix
    si({BLEFT,ANY,UP,ANY,ANY},BDown,'S');
    si({BDOWN,ANY,ANY,LEFT,ANY},BRight,'E');
    si({BRIGHT,ANY,ANY,ANY,DOWN},BUp,'N');
    si({BUP,RIGHT,ANY,ANY,ANY},BLeft,'W');
    // fix
    si({LEFT,BRIGHT,ANY,ANY,ANY},BLeft,'H');
    si({DOWN,ANY,BUP,ANY,ANY},BDown,'H');
    si({RIGHT,ANY,ANY,BLEFT,ANY},BRight,'H');
    si({UP,ANY,ANY,ANY,BDOWN},BUp,'H');
    // // shrink good
    // si({CAND,ANY&~RIGHT,BOUND,BOUND,DOWN},Path,'N');
    // si({CAND,RIGHT,BOUND,BOUND,ANY&~DOWN},Path,'W');
    // // cont shrink
    // si({LEFT,EMPTY|PATH,ANY,ANY,ANY},Cand,'H');
    // si({DOWN,ANY,EMPTY|PATH,ANY,ANY},Cand,'H');
    // si({RIGHT,ANY,ANY,EMPTY|PATH,ANY},Cand,'H');
    // si({UP,ANY,ANY,ANY,EMPTY|PATH},Cand,'H');
    // // shrink cont
    // si({CAND,ANY&~RIGHT,ANY&~UP,ANY&~LEFT,DOWN},Path,'N',true);
    // si({CAND,RIGHT,ANY&~UP,ANY&~LEFT,ANY&~DOWN},Path,'W',true);
    // si({CAND,ANY&~RIGHT,UP,ANY&~LEFT,ANY&~DOWN},Path,'S',true);
    // si({CAND,ANY&~RIGHT,ANY&~UP,LEFT,ANY&~DOWN},Path,'E',true);
    // // check
    // si({CAND,RIGHT,UP,ANY,ANY},Left,'W',true);
    // si({CAND,RIGHT,ANY&~UP,LEFT,ANY},Left,'W',true);
    // si({CAND,RIGHT,ANY&~UP,ANY&~LEFT,DOWN},Left,'W',true);
    // si({CAND,ANY&~RIGHT,UP,LEFT,ANY},Down,'S',true);
    // si({CAND,ANY&~RIGHT,UP,ANY&~LEFT,DOWN},Down,'S',true);
    // si({CAND,ANY&~RIGHT,ANY&~UP,LEFT,DOWN},Right,'E',true);
    // // extend
    // si({LEFT,PATH,ANY,ANY,ANY},Path,'H');
    // si({DOWN,ANY,PATH,ANY,ANY},Path,'H');
    // si({RIGHT,ANY,ANY,PATH,ANY},Path,'H');
    // si({UP,ANY,ANY,ANY,PATH},Path,'H');
}

first post :D

История