Finding strongly connected components with the cheriyan_mehlhorn_gabow algorithm in O ( V+E ) ================================================================================
- Rstack: We store nodes representing strongly connected components
- Ostack: We store the nodes that we pass through during the dfs implementation
- The strongly connected component is open: it is a component that includes an active contract
- The component connected to the force of the closure: it is the component of each node in the state of completion
- The new component: It is the component that we have not discovered yet, i.e. the contract is in new state
Init(G):
for each v∈V do
state[v]=new
dfs_counter=0
O_stack=∅
R_stack=∅
Depth First Search( ) :
Init(G)
for each v ∈V do
if ( state [ v ]=new )then
dfs( v )
Dfs ( v ) :
state [ v ]=active
dfs_num [ v ]=dfs_counter
dfs_counter=dfs_counter+1
O_stack .push ( v )
R_stack .push( v )
for each ( v ,w )∈E do
if ( state [ w ]=new )then
dfs( w )
else if ( w in O_stack ) then
while ( dfs_number [ w ]<〖dfs_number [ R〗_(stack ).top ( )])
R_stack.pop ( )
if ( v=R_stack .top ( ))
R_stack .pop ()
repeat
w=O_stack .pop ( )
component[w]=v
until v=w
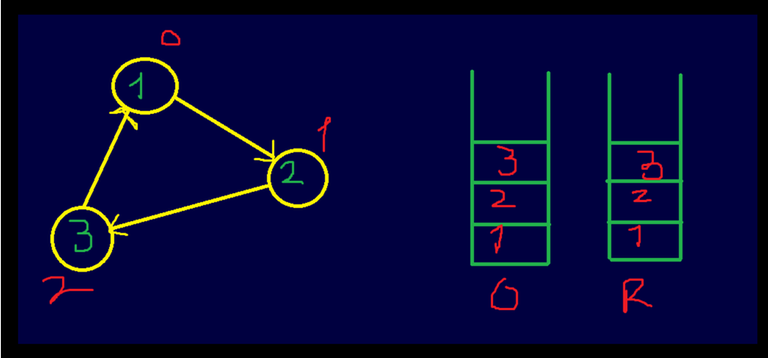
Explanation of how the algorithm works:
- For example, in this example, I applied dfs(0), when it reaches node 3, it will then move to 1, and I am visiting the 1 before, and therefore I have the possibility of
- Component represented by node 1. As long as the nodes in Ostack, starting from the last node inserted, have a detection time greater than 1, we delete them from Rstack.
- I mean, it is impossible for nodes to represent a strongly connected component (it is not impossible, but it is impossible here because dfs(0) was applied, which means that this thing is due to the behavior of dfs) and it is { 3 , 2 } , so it remains with Rstack { 1 } which is the representative of the strongly connected component , so select this thing b
- Backtract on the dfs, after we finish the dfs on it, I see if the first number in Rstack is the same node, then I do the same operation that I did on Rstack, but on Ostack, it means 3, 2, 1 strongly connected components, and the representative of this component is node 1, I keep deleting From Ostack until I get to the node that dfs just removed.
This means that the process of determining the representative of the strongly connected component will occur when the search is completed in a node when backtracking
-The Rstack is used to denote the representative, where when we move from node v to node w that we visited before q, we will delete all nodes that were discovered after this node, because any node that was discovered after it can be accessed through w, so the possibility of w being a representative of the component.
-So I just finished searching for a node, so follow dfs to do bactrack, and when I come back I see the following: The Ostack is just until I come back knowing that all the nodes that were discovered after the current node, of course, are the nodes that must be compatible with the first node in Rstack, which is a component Connected to the power represented by the current node.
My code in c++ :
#include <bits/stdc++.h>
using namespace std ;
#define all(object) object.begin(),object.end()
#define sz(object) (int)object.size()
#define pb push_back
#define ss second
#define ff first
typedef long long ll ;
ll INF =1e9;
inline void setIO(string name = "")
{
ios_base::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr); // see Fast Input & Output
if (sz(name))
{
freopen((name + ".in").c_str(), "r", stdin); // see Input & Output
freopen((name + ".out").c_str(), "w", stdout);
}
}
vector<int>adj[200005];
bool visit[200005];
bool In_Ostack [200005],In_Rstack[200005];
int dfs_Number [200005],comp[200005];
int dfs_Counter = 1;
stack <int>Ostack,Rstack;
int n , m ;
void dfs (int node)
{
visit[node]=true;
dfs_Number[node]=dfs_Counter ;
dfs_Counter +=1 ;
Ostack.push(node); In_Ostack[node]=true;
Rstack.push(node); In_Rstack[node]=true;
for (int child:adj[node])
{
if( !visit[child])
dfs(child);
else if (In_Ostack[child])
while (dfs_Number[child]<dfs_Number[Rstack.top()])
{
In_Rstack[Rstack.top()]=false;
Rstack.pop();
}
}
if ( node == Rstack.top())
{
In_Rstack[Rstack.top()]=false;
Rstack.pop();
while (node!=Ostack.top())
{
In_Ostack[Ostack.top()]=false;
comp[Ostack.top()]=node;
Ostack.pop();
}
In_Ostack[node]=false;
comp[node]=node;
Ostack.pop();
}
}
int main ( )
{
cin >> n >> m ;
for(int i=1,u,v;i<=m;i++)
{
cin>>u>>v;
adj[u].push_back(v);
}
for(int i=0;i<n;i++)
if(!visit[i])
dfs(i) ;
for (int i=0;i<n;i++)
cout <<comp[i]<<" " ;
}





