Nowcoder problem (Chinese) link
First I would like to thank ShaoNianTongXue5307 for his idea!
This is a learning note, most for myself. Most of this blog is not original.
Part 1: Problem Statement:
A tree $$$T=(V, E)$$$ has $$$n$$$ vertices and $$$n-1$$$ edges, the weight of each vertex $$$i$$$ is $$$a_i$$$.
For each edge $$$e$$$, you can determine its direction, i.e., for two vertices $$$u, v$$$, there are two states: $$$u \rightarrow v$$$ and $$$v \rightarrow u$$$. There are $$$2^{n-1}$$$ states in total.
For each state $$$S$$$, we define $$$f(S)$$$ as
$$$f(S) := \sum\limits_{(u, v) \in V \times V, v\,\text{is reachable from}\,u} |a_u - a_v|$$$.
Compute the sum of $$$f(S)$$$ over all $$$2^{n-1}$$$ states $$$S$$$, modulo $$$998244353$$$.
Example:
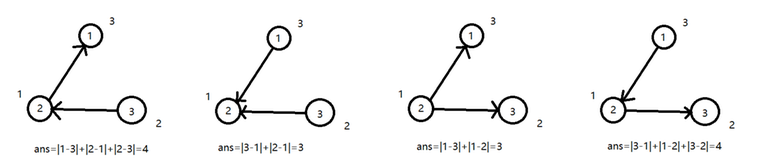
Suppose $$$n=3$$$, and two edges connect $$$(1, 2), (2, 3)$$$, respectively. $$$a_1 = 3, a_2 = 1, a_3 = 2$$$, the answer is $$$14$$$.
Constraints: $$$2 \leq n \leq 2 \cdot 10^5$$$, $$$1 \leq a_i \leq 10^9$$$.
Part 2: What is the centroid decomposition good at?
Before we learn centroid decomposition, we should first know what it is good at. For a tree $$$T = (V, E)$$$, we can decompose $$$V$$$ into $$$V = V_1 \cup V_2 \cup ... \cup V_t$$$, where $$$V_i (1 \leq i \leq t)$$$ are pairwise disjoint non-empty sets. $$$V_1$$$ is a singleton which contains only one element: The centroid. $$$V_2, ..., V_t$$$ are the connected components of $$$T \setminus V_1$$$. We want to calculate some function $$$f(T)$$$, and we assume that the base case, where $$$V(T) = 1$$$, is easy to calculate. This assumption is not strict, because if we can't even deal with the case where $$$V(T)=1$$$, we can actually achieve nothing. The another important function besides $$$f$$$ is the merge function: $$$merge(V_1, V_2, ..., V_t)$$$. Formally
$$$f(V) = \sum\limits_{i=1}^t f(V_i) + merge(V_1, V_2, ..., V_t)$$$. (1)
Like the merge sort, the number of iterations in the centroid decomposition algorithm is $$$O(log |V|)$$$, so it takes roughly $$$O(log |V| \cdot merge)$$$ times. Therefore, the most important advantage to use centroid decomposition is that the merge function could be computed fast enough. Otherwise, it is even slower than the brute force! In our solution merge is $$$O(|V|log|V|)$$$ so its complexity is $$$O(|V|log^2|V|)$$$.
Part 3: What is a centroid, and what is a centroid decomposition?
For a tree, the vertex $$$v$$$ is called a centroid if and only if for any subtree rooted at v’s child has a size at most half the size of the original tree rooted at $$$v$$$. For example, the centroids for the path A--B--C--D are B and C.
Property $$$1$$$: A tree has one or two centroids. This property can be generalized to the positive weighted tree.
Proof: First, we prove that one tree has at least one centroid. The centroid could be found using a constructive algorithm. First we specify an original root $$$r$$$. Initialize $$$v$$$ as $$$r$$$. Check whether $$$v$$$ is a centroid. If yes, we have already done. If not, replace $$$v$$$ with $$$v$$$'s heavy child, i.e., $$$arg\max\{size[u]|u \text{is} v\text{'s child}\}$$$.






