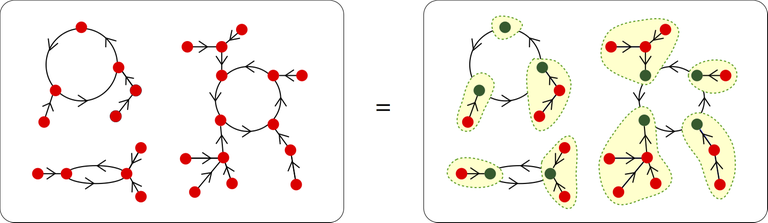
Hi everyone!
In my previous blog, I wrote about how generating functions can be used to enumerated labeled species. In this blog, I want to continue the topic by writing about how one can account for different kinds of symmetries when counting different combinatorial structures. Ultimately, we will end up deriving and hopefully understanding the analogue of Pólya enumeration theorem in species.
Difficulty: ★★★★☆
Prerequisites:
- Familiarity with combinatorial species (see my prev. blog), OR
- Very good intuition with enumerative combinatorics, genfuncs and recap below.
I will try to use plain language rather than formulas as much as possible, as it seems to be the preferred format for readers.
Recap
Below is a very brief recap of the most important things from the previous article. I tried to keep it as informal as possible.
If $$$A(x)$$$ and $$$B(x)$$$ are the generating functions for species $$$A$$$ and $$$B$$$, then $$$A(B(x))$$$ is the generating function for their composition.
It is a fundamental result for labeled species. Unfortunately, there is no simple analogue with unlabeled structures, and deriving the composition formula in some reasonable formulation for them is the ultimate goal of this article.
How unlabeled structures work
Let's take a closer look on the equivalence classes that are formed when we enumerate unlabeled structures. What is common for the elements of an equivalence class? How to compute the size of an equivalence class? How to enumerate the elements of a given equivalence class, if a single representative is known?
Let $$$|A|=n$$$. Consider an object $$$o \in F(A)$$$ of the species $$$F$$$. If we use a permutation $$$\sigma : A \to A$$$ on the underlying set of atoms, it will produce a new object $$$F_\sigma(o)$$$. There is a total of $$$n!$$$ possible permutations $$$\sigma$$$ of $$$n$$$ atoms, and when we apply $$$F_\sigma$$$ to a specific object $$$o$$$ for all permutations $$$\sigma$$$, we obtain all the elements of its equivalence class defined above.
Claim 1. For every object $$$o'$$$ that may be produced as a result of applying $$$F_\sigma$$$ to $$$o$$$, the number of permutations $$$\sigma$$$ that produce $$$o'$$$ is the same as the number of permutations that produce $$$o$$$ itself.
Explanation. Let $$$\tau$$$ be a permutation such that $$$F_\tau(o) = o'$$$. Then for any permutation $$$\sigma$$$ such that $$$F_\sigma(o)=o$$$, there is a permutation $$$\tau \circ \sigma$$$ such that $$$F_{\tau \circ \sigma}(o) = F_\tau(F_\sigma(o)) = o'$$$. Same is true in the other direction.
The permutations $$$\sigma$$$ such that $$$F_\sigma(o)=o$$$ are called the automorphisms of the object $$$o$$$. So among $$$n!$$$ values of $$$F_\sigma(o)$$$, if we consider them as a multiset, each unique one is counted $$$|\operatorname{Aut}(o)|$$$ times, where $$$\operatorname{Aut}(o) = \{\sigma : F_\sigma(o) = o\}$$$ is the set of automorphisms of $$$o$$$.
This allows us to say that the size of the equivalence class of $$$o$$$ is exactly $$$\frac{n!}{|\operatorname{Aut}(o)|}$$$.
Burnside lemma
The result above is very useful, as now instead of counting the number of equivalence classes we instead can "distribute" the counting among all the elements, that is we may represent the total number of equivalence classes as
In this way, the elements from the same equivalence class, when summed up together, will produce $$$1$$$.
On the other hand, the sum of $$$|\operatorname{Aut}(o)|$$$ can be reformulated as follows:
where $$$\operatorname{Fix}(\sigma)$$$ is the number of fixed points of $$$F_\sigma$$$, that is $$$\operatorname{Fix}(\sigma) = \{o \in F(A) : F_\sigma(o) = o\}$$$.
This gives the following alternative formula for the number of the equivalence classes:
also known as the Burnside lemma. That being said, the number of unlabeled structure on $$$n$$$ atoms of the species equates to the average number of fixed points over all permutations of length $$$n$$$. This key observation allows us to apply key properties of expected values to compute the number of equivalence classes, in particular use the linearity of expected value.
Automorphisms and fixed points for compositions
To construct an $$$F \circ G$$$ structure, we first build an $$$F$$$-structure on a set $$$B = \{1, 2, \dots, k\}$$$, and then substitute the $$$i$$$-th of its atoms with a $$$G$$$-structure built on the set $$$A_i$$$. Then, we treat the disjoint union $$$A = A_1 \sqcup A_2 \sqcup \dots \sqcup A_k$$$ as the full set of atoms. So, an object $$$o$$$ of species $$$F \circ G$$$ can be described by an object $$$f \in F(B)$$$ and a family of objects $$$g_1, \dots, g_k$$$, where $$$g_i \in G(A_i)$$$.
Automorphisms of a given object
Consider a permutation $$$\sigma : A \to A$$$. What should hold for it to be an automorphism of $$$o$$$?
First of all, it should preserve the structure of $$$f$$$. The object $$$f$$$ is built on top of the sets $$$A_1, \dots, A_k$$$, and to preserve the structure of $$$f$$$, the permutation $$$\sigma$$$ should only map these sets to each other. In other words, it should map a set $$$A_i$$$ to a set $$$A_j$$$ such that $$$|A_i| = |A_j|$$$, and the function $$$\rho(i) = j$$$ defined from such mapping should be a permutations, which is, in turn, an automorphism of $$$f$$$.
Then, if we look on a transition from $$$A_i$$$ to $$$A_{\rho(i)}$$$, the permutation $$$\sigma$$$ should be consistent with the mapping $$$\rho$$$. In other words, if we restrict the domain of $$$\sigma$$$ from the whole $$$A$$$ to its subset $$$A_i$$$, the resulting mapping $$$\sigma_i$$$ should map the object $$$g_i$$$ into the object $$$g_{\rho(i)}$$$.
That being said, each permutation of interest $$$\sigma : A \to A$$$ can be described by a permutation $$$\rho : B \to B$$$, which is an automorphism of $$$f$$$, and a family of bijections $$$\sigma_i : A_i \to A_{\rho(i)}$$$, such that $$$\sigma_i$$$ maps $$$g_i$$$ to $$$g_{\rho(i)}$$$.
Fixed points of a given permutation
Such setting allows us to think about what should hold for an object $$$o \in (F \circ G)(A)$$$ to be a fixed point of $$$\sigma$$$?
- The object $$$f$$$ must be a fixed point of $$$\rho$$$;
- For each $$$\sigma_i : A_i \to A_{j}$$$ it must hold that $$$F_{\sigma_i}(g_i) = g_{j}$$$.
The first criteria is understandable and is in line with what we have studied so far. What about the second, though? When is it true?
Essentially, it means that in a cycle decomposition of the permutation $$$\rho$$$, for each cycle $$$i_1 \to i_2 \to \dots \to i_m \to i_1$$$ we're allowed to choose a single distinct element $$$g_{i_1}$$$ in such way that it is a fixed point of a permutation $$$\tau = \sigma_{i_m} \circ \dots \circ \sigma_{i_2} \circ \sigma_{i_1}$$$, and all the other ones will be uniquely defined by the mappings $$$\sigma_{i_1}, \sigma_{i_2}, \dots, \sigma_{i_{m-1}}$$$.
Objects $$$g_{i_1}, \dots, g_{i_m}$$$ on a cycle $$$i_1 \to i_2 \to \dots \to i_m \to i_1$$$
Let $$$|A_{i_1}|= \dots = |A_{i_m}|=t$$$. What do we get if we average the amount of fixed points $$$g_{i_1}$$$ of $$$\tau$$$ over all permutations $$$\tau$$$? It follows from the Burnside lemma that we get the number of distinct unlabeled structures of species $$$G$$$ on $$$t$$$ atoms. The neat part here is that for each cycle in $$$\rho$$$ it could be done independently, multiplying the amounts to get the average amount for a fixed permutation $$$\rho$$$.
Averaging over all permutations
In other words, to count the average amount of fixed points of $$$\sigma : A \to A$$$, we can do the following:
- Consider a permutation $$$\rho : B \to B$$$;
- Pick a fixed point of $$$F_\rho$$$ as an $$$F$$$-structure;
- For each cycle of $$$\rho$$$, pick an unlabeled structure $$$g$$$ of $$$G$$$ and duplicate it on the whole cycle $$$g_{i_1}, \dots, g_{i_m}$$$;
- Average the counts over all permutations $$$\rho$$$ by dividing with $$$k!$$$.
These considerations boil down to the following essential formula:
where $$$\rho_j$$$ is the number of cycles of length $$$j$$$ in $$$\rho$$$, and the ordinary generating functions $$$G(x)$$$ and $$$(F \circ G)(x)$$$ are defined as
In other words, the functions are defined in such way that $$$[x^n]G(x)$$$ and $$$[x^n](F \circ G)(x)$$$ are the numbers of unlabeled $$$G$$$-structures and $$$(F \circ G)$$$-structures correspondingly on $$$n$$$ atoms, corresponding to OGFs defined for unlabeled structures in the previous article.
Intuitively, $$$G(x^j)$$$ is a generating functions for sets of $$$j$$$ equal unlabeled structures of species $$$G$$$, so we pick $$$|c|$$$ same $$$G$$$-structures for each cycle $$$c$$$ of length $$$|c|$$$ and then multiply the generating functions over all cycles, as it is done independently.
If you're not convinced yet, you can find a bit more technical and rigorous (but less intuitive) computation below to get the same result.
Cycle index series
looking on the formula above, we may define a multivariate formal power series
which allows to rewrite $$$(F \circ G)(x)$$$ as the formal power series composition:
The multivariate power series $$$Z_F(t_1, t_2, t_3, \dots)$$$ is called the cycle index series of the species $$$F$$$ and it holds a tremendous amount of information about the structure of the species. In particular, we may note that the exponential generating function of the species is simply
As to count labeled structures it is sufficient to count the fixed points of identity permutations (for which all cycles have length $$$1$$$).
and the ordinary generating function of unlabeled structures of the species is nothing but
as we may perceive the species as a composition of itself with an "atom" species $$$x$$$.
This is the composition formula for the unlabeled structures that we sought for.
Why is it called a cycle index series?
The definition of a cycle index series above may be rewritten in terms of automorphisms:
where $$$B_k = \{1, 2, \dots, k\}$$$.
Substituting $$$\frac{1}{k!} = \frac{|\operatorname{Aut}(o)|}{k!} \frac{1}{|\operatorname{Aut}(o)|}$$$, and recalling that the equivalence class of $$$o$$$ has $$$\frac{k!}{|\operatorname{Aut}(o)|}$$$ objects, we may rewrite the sum above as
where $$$\widetilde{F}(B_k)$$$ is the set of representatives of unlabeled equivalence classes of $$$F(B_k)$$$.
For a given set of permutations that is closed under composition (so-called permutation group) $$$G$$$, the polynomial
is known more widely as the cycle index of $$$G$$$. That being said, the cycle index series $$$Z_F(t_1, t_2, \dots)$$$ is the formal sum of cycle indices over all unlabeled structures of the species $$$F$$$ of all possible sizes.
Atom colorings
Note that for in all discussions above we assumed that either all atoms are distinct from each other (labeled) or indistinguishable (unlabeled). In a bit more generic setting we may assume that each atom is colored in one of $$$s$$$ distinct colors.
In this case, the number of indistinguishable structures built on such set of atoms is $$$Z(G)(s, s, \dots, s)$$$, as we enumerated fixed points of $$$\rho$$$ by coloring all atoms on each cycle in the same color.
Correspondingly, if we want to also keep track of the total number of atoms in cycle index series, we should use
Then, the coefficient $$$[x^n] f(s)$$$ will denote the number of $$$F$$$-structure on $$$n$$$ atoms, such that each atom is colored in one of $$$s$$$ distinct colors.
Examples
There are two famous species $$$F$$$ with known composition formulas. Specifically, the cycles and sets.
Let's derive explicit form for their cycle index series, and from that obtain the operators $$$\operatorname{CYC}$$$ and $$$\operatorname{MSET}$$$:
Cycles
Consider a cycle of length $$$n$$$. What do its automorphisms look like? Its automorphisms are:
- A permutation with this cycle as its cycle presentation;
- Powers of this permutation.
This is a total of $$$n$$$ elements. When we raise the cycle to the power $$$k$$$, we obtain a set of $$$\gcd(k, n)$$$ of length $$$n/\gcd(n, k)$$$ each.
For example, raising single cyclic shift $$$[2,3,4,5,6,1]$$$ with cycle presentation $$$(1~2~3~4~5~6)$$$ to the power $$$3$$$, we get a permutation $$$[4,5,6,1,2,3]$$$ with a cycle presentation $$$(1~4)(2~5)(3~6)$$$. Note that all cycles of length $$$n$$$ are isomorphic to each other, meaning that there is a unique unlabeled cycle of length $$$n$$$ with the cycle index
The last formula is due to the fact that there are $$$\varphi(\frac{n}{d})$$$ numbers $$$k$$$ such that $$$\gcd(k, n) = d$$$. If we sum it up over all $$$n$$$, we get
then substituting $$$k=\frac{n}{d}$$$, we get
making it into
From this, the unlabeled composition formula of $$$\operatorname{CYC}$$$ species of cycles and arbitrary species $$$f$$$ with OGF $$$f(x)$$$ is:
Sets
Now, in case of sets, we would get the same set no matter how we rearrange its elements. Again, there is a unique unlabeled set on $$$n$$$ vertices, and its automorphisms are all possible permutations, hence we have
Assuming that there are $$$j_k$$$ cycles of length $$$k$$$, the formula above rewrites as
Indeed, the number of ways to make a permutation with given $$$j_1, \dots, j_n$$$ is
as for $$$j_k$$$ cycles of length $$$k$$$, you divide by $$$k^{j_k}$$$ to not double-count cyclic shifts and by $$$j_k!$$$ to not double-count rearrangements of cycles.
On the other hand, if we sum it up over all $$$n$$$, we get
Adding a new variable $$$y$$$ to track the sum of $$$j_1 + 2j_2 + \dots + n j_n$$$, we can rewrite it as product of sums:
Finally, substituting $$$y=1$$$, we get the sum over all possible $$$n$$$ as
and the composition formula with set species
The results above also yield simplified expression for $$$Z(S_n)$$$:
Cycle index composition
In a very generic setting, one may prove the general formula:
Derivation, explanation and proof of this formula is left to the reader as an exercise.
Further reading
Asymmetry index series
In this article, we studied how to account for symmetries (automorphisms) when we transition from enumerating labeled structures to enumerating unlabeled ones. Another use-case which is worth studying are so-called asymmetric structures, that is the structures that only have the identity permutation as their single automorphism. In such structures, any unlabeled structure has exactly $$$n!$$$ ways to turn it into a labeled one, meaning that the OGF of the unlabeled structures and the EGF of corresponding labeled structures coincide.
In a similar fashion, it is possible to introduce a so-called "asymmetry index series", which we may then use to compose operators like $$$\operatorname{CYC}$$$ and $$$\operatorname{SET}$$$ on the generating functions of asymmetric structures. Maybe I will write more about it in future blog entries...