Problem: [Rectangle Shrinking](https://codeforces.me/problemset/problem/1782/e)↵
↵
Part 1: **Notations**↵
↵
$x$: A brick. $x_i$ denotes the part of $x$ belonging to the $i$-th floor. For example, if $x.u=1,\,x.d=2$, then $x_1.u=x_1.d=1$, $x_2.u=x_2.d=2$, and $x_1.l=x_2.l=x.l$, $x_1.r=x_2.r=x.r$.↵
↵
$A_i,\,i=1,2$: The set of bricks whose $u=d=i$.↵
↵
$B$: The set of bricks whose $u=1,\,d=2$.↵
↵
$\texttt{Remove}$: Remove a brick $x$.↵
↵
$\texttt{Shrink}$: Shrink a brick $x$ to another **non-empty** brick.↵
↵
$\texttt{Keep}$: Keep a brick $x$ unchanged.↵
↵
Note that in our solution we may operate on a part of brick. For example, for a brick $x \in B$, we may $\texttt{Keep}\,x_1$ while $\texttt{Remove}\,x_2$.↵
↵
Part 2: **Idea**↵
↵
I think $\texttt{Shrink}$ing $x \in B$ is troublesome. If you shrink $x_1$, you have to shrink $x_2$ in the same way, i.e., $x_1$ has to be aligned with $x_2$. So is there a solution that only performs $\texttt{Remove}$ and $\texttt{Keep}$ on every $x \in B$? But that is impossible, because the bricks $x, y \in B$ may overlap themselves even with considering $A$. So what if $B$ are pairwise non-overlapping (because we could perform some pre-$\texttt{Shrink}$ and pre-$\texttt{Remove}$ to make $B$ pairwise non-overlapping)? [Pre-computation]↵
↵
In that case, we can consider each floor independently. Let ↵
↵
$C_i := A_i \cup \\{x_i \mid x \in B \\}$. ↵
↵
For example, if ↵
↵
$A_1 = \\{[u=1, d=1, l=2, r=5], [u=1, d=1, l=7, r=10]\\}$, ↵
↵
$B=\\{[u=1, d=2, l=2, r=2], [u=1, d=2, l=4, r=7]\\}$, then ↵
↵
$C_1 = \\{[u=1, d=1, l=2, r=2], [u=1, d=1, l=2, r=5], [u=1, d=1, l=4, r=7], [u=1, d=1, l=7, r=10]\\}$. ↵
↵
We sort $C_i$ w.r.t $l$, and traverse $C_i$ like $\texttt{for(auto x: C_i)}$. ↵
↵
Case 1 ($\texttt{Keep}$): If $x$ is not overlapping now, then we add $x$ to the answer, no matter if $x$ is from $A_i$ or not. ↵
↵
Case 2 ($\texttt{Remove}$): If $x$ is fully contained in the union of other rectangles, then we always remove $x$, no matter if $x$ is from $A_i$ or not. ↵
↵
$\texttt{Keep}$ and $\texttt{Remove}$ are relatively easier, no matter $x \in A_i$ or $x \in \\{x_i \mid x \in B \\}$.↵
↵
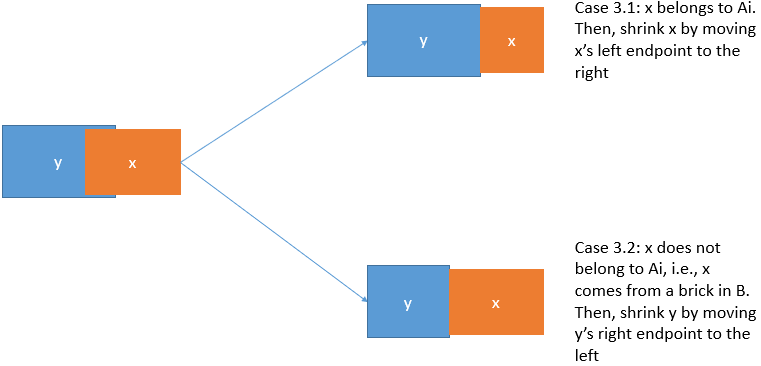
Case 3 ($\texttt{Shrink}$): If $x$ is partially overlapping with other bricks.↵
↵
Case 3.1: If $x \in A_i$: $\texttt{Shrink} x$. Move the $x.l$ to the right to avoid overlapping.↵
↵
Case 3.2: If $x \in \\{x_i \mid x \in B \\}$: $\texttt{Shrink}$ all bricks that overlap with $x$ by moving their right endpoints (i.e., *.r), to the left.↵
↵
↵
↵
It is guaranteed in Case 3.2 that every brick overlapping with $x$ is from $A_i$ because we have already performed pre-calculations in $B$ to make them non-overlapping. The complexity is not an issue, by amortized analysis, each $x \in A_i$ will do $\texttt{Remove}$ at most once and $\texttt{Remove}+\texttt{Shrink}$ at most twice (keep/move left endpoint+keep/move right endpoint). ↵
↵
Part 3: **Implementation**↵
↵
First I copy a range-set [implementation](https://atcoder.jp/contests/arc151/submissions/35725980) from [user:nok0,2023-01-18]. Basically, it maintains a set of intervals using $\texttt{std::set}$. When inserting/erasing a range, it can merge/split/erase intervals automatically, using binary search (Yes, stop learning useless algorithms, go to learn binary search!). It supports many APIs, here are some useful APIs in our implementation:↵
↵
(1) $\texttt{Insert(l, r)}$: Insert an interval $[l, r]$.↵
↵
(2) $\texttt{covered_by(l, r)}$: Return an interval covering $[l, r]$, if not exists, returning $(-\infty, \infty)$.↵
↵
(3) $\texttt{covered(l, r)}$: Return a bool variable indication whether interval $[l, r]$ is fully covered. ↵
↵
(4) $\texttt{right(x)}$: Return $\min \\{y|y \geq x, y \text{ is not covered}\\}$. Note that API could calculate the $\texttt{mex}$, so it is also useful for calculating the [Sprague-Grundy (SG) number](https://en.wikipedia.org/wiki/Sprague%E2%80%93Grundy_theorem). SG number is irrelevant to our topic.↵
↵
(5) $\texttt{left(x)}$ (added by me): Return $\max \\{y|y \leq x, y \text{ is not covered}\\}$.↵
↵
There are also APIs that we don't use in this implementation, but they are also beneficial:↵
↵
(6) $\texttt{Erase(l, r)}$: Erase $[l, r]$. That may lead to interval splitting, for example, if we erase $[2, 3]$ from $[1, 4]$, we get two intervals remaining: $[1, 1]$ and $[4, 4]$.↵
↵
(7) $\texttt{size}$: Get the size of intervals.↵
↵
(8) $\texttt{dump}$: Output all intervals for debugging.↵
↵
So, we implement the pre-computation step (first paragraph in Part2) as follows:↵
↵
~~~~~↵
sort B w.r.t l (left endpoint).↵
Initial a range set named rs.↵
for(auto& x: B){↵
int rightl = rs.right(x.l), leftr = rs.left(x.r);↵
if(right <= rightr){↵
rs.insert(rightl, leftr);↵
for(int i = 1; i <= 2; ++i) {↵
Ci = Ai; Ci.push_back({x.u, x.rightl, x.d, x.leftr, x.id}); //push into Ci↵
}↵
}else{↵
//Case 2, fully contained, remove it!↵
//We actually do nothing here↵
}↵
} ↵
~~~~~↵
↵
Then, how to calculate $C_i$ from each floor independently? We need another set that is sorted by $r$ in the ascending order, let's call it $\texttt{sortbyr}$, to maintain rectangles in $A_i \subseteq C_i$. If Case 3.2 happens, we need to find such $y \in \texttt{sortbyr}$ quickly by $\texttt{sortbyr.lower_bound(x.l)}$, i.e., find an interval $y \in A_i$ quickly, using binary search, such that the right endpoint of $y$ ($y.r$) is greater or equal than $x.l$. Note that when we find such an $y$, you need to iterate to the end of $\texttt{sortbyr}$, that's why my previous submissions WA at test15--I only handle **one of them**. Here is the sketch of the implementation:↵
↵
~~~~~↵
for(int i = 1; i <= 2; ++i){↵
Initialize sortbyr; //Remember to initialize because we handle each floor independently!↵
sort(Ci.begin(), Ci.end());↵
Initial a range set named rs.↵
for(auto x: Ci){↵
bool lcovered = rs.covered(l), rcovered = rs.covered(r);↵
if(!lcovered && !rcovered){↵
//Case 1, Keep↵
if(u == d){↵
sortbyr.insert({x.u, x.l, x.d, x.r, x.id});↵
}↵
ans[x.id].insert(node{j+1, x.l, j+1, x.r, x.id}); //No matter u == d or u != d, we only consider one floor here!↵
rs.insert(x.l, x.r);↵
}else if(lcovered && !recovered){↵
if(u == d){↵
//Case 3.1↵
int rightl = rs.right(l);↵
ans[x.id].insert(x.u, x.rightl, x.d, x.r, x.id);↵
rs.insert(rightl, x.r);↵
sortbyr.insert(x.u, x.rightl, x.d, x.r, x.id});↵
}else{↵
//Case 3.2↵
auto y = sortbyr.lower_bound({-1, -1, -1, x.l, -1});↵
while(y != sortbyr.end()){↵
//Here, we should deal with all overlaps! That's why my previous submissions WA on test15↵
auto [u2, l2, d2, r2, id2] = *y;↵
//Here l2 <= l because we sort Ci by l. So sortbyr only contains elements whose left endpoint <= l!↵
//By lower_bound, we have r2 >= x.l↵
ans[id2].erase({u2, l2, d2, r2, id2}); //We erase it from our answer↵
sortbyr.erase(y++);↵
ans[x.id].insert({j+1, x.l, j+1, x.r, x.id}); //We never shrink the splitted ones↵
rs.insert(x.l, x.r); //Although [l, r] overlaps with [l2, r2], range set will merge them automatically!↵
if(l2 <= l-1){ //Be careful! r2 may <= r, so y after shrinking may be empty!! ↵
ans[id2].insert({u2, l2, d2, x.l-1, id2});↵
sortbyr.insert({u2, l2, d2, x.l-1, id2});↵
}↵
}↵
}//Case 3.2↵
}//Case 3↵
}//for↵
}↵
~~~~~↵
↵
In the above implementation, it is not possible that $\texttt{!lcovered && rcovered}$, otherwise $[l, r]$ is covered by some $[l_1, r_1]$ which $l_1 > l$. But we have already sorted $C_i$ by $l$. And, if $l$ and $r$ are both covered, we just ignore and \texttt{Remove} this segment.↵
↵
Finally, we need to output the answer, for this part please refer to the [code](https://codeforces.me/contest/1782/submission/189601171). Note that due to the implementation, we may insert two parts of bricks for $b \in B$. I mean, for $x = \\{1, l, 2, r, id\\} \in B$, the implementation might insert both $\\{1, l, 1, r, id\\}$ and $\\{2, l, 2, r, id\\}$ into $ans[id]$, so we need to merge them manually, that is dirty work.↵
↵
Here is an advertisement for CFStress: Although my [previous submission](https://codeforces.me/contest/1782/submission/189433130) WA on case5 of test15, [CFStress](https://cfstress.com/status/16701) could still find a very small counterexample in a very short time! As mentioned [here](https://codeforces.me/blog/entry/110936), My debugging ability is really poor, so I don't use CFStress very frequently, as I often debug myself to improve my debugging ability. However, CFStress has saved me many times from insomnia. Thanks, [user:variety-jones,2023-01-18]!↵
↵
↵
↵
↵
↵
↵
↵
↵
Part 1: **Notations**↵
↵
$x$: A brick. $x_i$ denotes the part of $x$ belonging to the $i$-th floor. For example, if $x.u=1,\,x.d=2$, then $x_1.u=x_1.d=1$, $x_2.u=x_2.d=2$, and $x_1.l=x_2.l=x.l$, $x_1.r=x_2.r=x.r$.↵
↵
$A_i,\,i=1,2$: The set of bricks whose $u=d=i$.↵
↵
$B$: The set of bricks whose $u=1,\,d=2$.↵
↵
$\texttt{Remove}$: Remove a brick $x$.↵
↵
$\texttt{Shrink}$: Shrink a brick $x$ to another **non-empty** brick.↵
↵
$\texttt{Keep}$: Keep a brick $x$ unchanged.↵
↵
Note that in our solution we may operate on a part of brick. For example, for a brick $x \in B$, we may $\texttt{Keep}\,x_1$ while $\texttt{Remove}\,x_2$.↵
↵
Part 2: **Idea**↵
↵
↵
In that case, we can consider each floor independently. Let ↵
↵
$C_i := A_i \cup \\{x_i \mid x \in B \\}$. ↵
↵
For example, if ↵
↵
$A_1 = \\{[u=1, d=1, l=2, r=5], [u=1, d=1, l=7, r=10]\\}$, ↵
↵
$B=\\{[u=1, d=2, l=2, r=2], [u=1, d=2, l=4, r=7]\\}$, then ↵
↵
$C_1 = \\{[u=1, d=1, l=2, r=2], [u=1, d=1, l=2, r=5], [u=1, d=1, l=4, r=7], [u=1, d=1, l=7, r=10]\\}$. ↵
↵
We sort $C_i$ w.r.t $l$, and traverse $C_i$ like $\texttt{for(auto x: C_i)}$. ↵
↵
Case 1 ($\texttt{Keep}$): If $x$ is not overlapping now, then we add $x$ to the answer, no matter if $x$ is from $A_i$ or not. ↵
↵
Case 2 ($\texttt{Remove}$): If $x$ is fully contained in the union of other rectangles, then we always remove $x$, no matter if $x$ is from $A_i$ or not. ↵
↵
$\texttt{Keep}$ and $\texttt{Remove}$ are relatively easier, no matter $x \in A_i$ or $x \in \\{x_i \mid x \in B \\}$.↵
↵
Case 3 ($\texttt{Shrink}$): If $x$ is partially overlapping with other bricks.↵
↵
Case 3.1: If $x \in A_i$: $\texttt{Shrink} x$. Move the $x.l$ to the right to avoid overlapping.↵
↵
Case 3.2: If $x \in \\{x_i \mid x \in B \\}$: $\texttt{Shrink}$ all bricks that overlap with $x$ by moving their right endpoints (i.e., *.r), to the left.↵
↵
↵
↵
It is guaranteed in Case 3.2 that every brick overlapping with $x$ is from $A_i$ because we have already performed pre-calculations in $B$ to make them non-overlapping. The complexity is not an issue, by amortized analysis, each $x \in A_i$ will do $\texttt{Remove}$ at most once and $\texttt{Remove}+\texttt{Shrink}$ at most twice (keep/move left endpoint+keep/move right endpoint). ↵
↵
Part 3: **Implementation**↵
↵
First I copy a range-set [implementation](https://atcoder.jp/contests/arc151/submissions/35725980) from [user:nok0,2023-01-18]. Basically, it maintains a set of intervals using $\texttt{std::set}$. When inserting/erasing a range, it can merge/split/erase intervals automatically, using binary search (Yes, stop learning useless algorithms, go to learn binary search!). It supports many APIs, here are some useful APIs in our implementation:↵
↵
(1) $\texttt{Insert(l, r)}$: Insert an interval $[l, r]$.↵
↵
(2) $\texttt{covered_by(l, r)}$: Return an interval covering $[l, r]$, if not exists, returning $(-\infty, \infty)$.↵
↵
(3) $\texttt{covered(l, r)}$: Return a bool variable indication whether interval $[l, r]$ is fully covered. ↵
↵
(4) $\texttt{right(x)}$: Return $\min \\{y|y \geq x, y \text{ is not covered}\\}$. Note that API could calculate the $\texttt{mex}$, so it is also useful for calculating the [Sprague-Grundy (SG) number](https://en.wikipedia.org/wiki/Sprague%E2%80%93Grundy_theorem). SG number is irrelevant to our topic.↵
↵
(5) $\texttt{left(x)}$ (added by me): Return $\max \\{y|y \leq x, y \text{ is not covered}\\}$.↵
↵
There are also APIs that we don't use in this implementation, but they are also beneficial:↵
↵
(6) $\texttt{Erase(l, r)}$: Erase $[l, r]$. That may lead to interval splitting, for example, if we erase $[2, 3]$ from $[1, 4]$, we get two intervals remaining: $[1, 1]$ and $[4, 4]$.↵
↵
(7) $\texttt{size}$: Get the size of intervals.↵
↵
(8) $\texttt{dump}$: Output all intervals for debugging.↵
↵
So, we implement the pre-computation step (first paragraph in Part2) as follows:↵
↵
~~~~~↵
sort B w.r.t l (left endpoint).↵
Initial a range set named rs.↵
for(auto& x: B){↵
int rightl = rs.right(x.l), leftr = rs.left(x.r);↵
if(right <= rightr){↵
rs.insert(rightl, leftr);↵
for(int i = 1; i <= 2; ++i) {↵
Ci = Ai; Ci.push_back({x.u, x.rightl, x.d, x.leftr, x.id}); //push into Ci↵
}↵
}else{↵
//Case 2, fully contained, remove it!↵
//We actually do nothing here↵
}↵
} ↵
~~~~~↵
↵
Then, how to calculate $C_i$ from each floor independently? We need another set that is sorted by $r$ in the ascending order, let's call it $\texttt{sortbyr}$, to maintain rectangles in $A_i \subseteq C_i$. If Case 3.2 happens, we need to find such $y \in \texttt{sortbyr}$ quickly by $\texttt{sortbyr.lower_bound(x.l)}$, i.e., find an interval $y \in A_i$ quickly, using binary search, such that the right endpoint of $y$ ($y.r$) is greater or equal than $x.l$. Note that when we find such an $y$, you need to iterate to the end of $\texttt{sortbyr}$, that's why my previous submissions WA at test15--I only handle **one of them**. Here is the sketch of the implementation:↵
↵
~~~~~↵
for(int i = 1; i <= 2; ++i){↵
Initialize sortbyr; //Remember to initialize because we handle each floor independently!↵
sort(Ci.begin(), Ci.end());↵
Initial a range set named rs.↵
for(auto x: Ci){↵
bool lcovered = rs.covered(l), rcovered = rs.covered(r);↵
if(!lcovered && !rcovered){↵
//Case 1, Keep↵
if(u == d){↵
sortbyr.insert({x.u, x.l, x.d, x.r, x.id});↵
}↵
ans[x.id].insert(node{j+1, x.l, j+1, x.r, x.id}); //No matter u == d or u != d, we only consider one floor here!↵
rs.insert(x.l, x.r);↵
}else if(lcovered && !recovered){↵
if(u == d){↵
//Case 3.1↵
int rightl = rs.right(l);↵
ans[x.id].insert(x.u, x.rightl, x.d, x.r, x.id);↵
rs.insert(rightl, x.r);↵
sortbyr.insert(x.u, x.rightl, x.d, x.r, x.id});↵
}else{↵
//Case 3.2↵
auto y = sortbyr.lower_bound({-1, -1, -1, x.l, -1});↵
while(y != sortbyr.end()){↵
//Here, we should deal with all overlaps! That's why my previous submissions WA on test15↵
auto [u2, l2, d2, r2, id2] = *y;↵
//Here l2 <= l because we sort Ci by l. So sortbyr only contains elements whose left endpoint <= l!↵
//By lower_bound, we have r2 >= x.l↵
ans[id2].erase({u2, l2, d2, r2, id2}); //We erase it from our answer↵
sortbyr.erase(y++);↵
ans[x.id].insert({j+1, x.l, j+1, x.r, x.id}); //We never shrink the splitted ones↵
rs.insert(x.l, x.r); //Although [l, r] overlaps with [l2, r2], range set will merge them automatically!↵
if(l2 <= l-1){ //Be careful! r2 may <= r, so y after shrinking may be empty!! ↵
ans[id2].insert({u2, l2, d2, x.l-1, id2});↵
sortbyr.insert({u2, l2, d2, x.l-1, id2});↵
}↵
}↵
}//Case 3.2↵
}//Case 3↵
}//for↵
}↵
~~~~~↵
↵
In the above implementation, it is not possible that $\texttt{!lcovered && rcovered}$, otherwise $[l, r]$ is covered by some $[l_1, r_1]$ which $l_1 > l$. But we have already sorted $C_i$ by $l$. And, if $l$ and $r$ are both covered, we just ignore and \texttt{Remove} this segment.↵
↵
Finally, we need to output the answer, for this part please refer to the [code](https://codeforces.me/contest/1782/submission/189601171). Note that due to the implementation, we may insert two parts of bricks for $b \in B$. I mean, for $x = \\{1, l, 2, r, id\\} \in B$, the implementation might insert both $\\{1, l, 1, r, id\\}$ and $\\{2, l, 2, r, id\\}$ into $ans[id]$, so we need to merge them manually, that is dirty work.↵
↵
Here is an advertisement for CFStress: Although my [previous submission](https://codeforces.me/contest/1782/submission/189433130) WA on case5 of test15, [CFStress](https://cfstress.com/status/16701) could still find a very small counterexample in a very short time! As mentioned [here](https://codeforces.me/blog/entry/110936), My debugging ability is really poor, so I don't use CFStress very frequently, as I often debug myself to improve my debugging ability. However, CFStress has saved me many times from insomnia. Thanks, [user:variety-jones,2023-01-18]!↵
↵
↵
↵
↵
↵
↵
↵





