This (quite sudden) post is about a data structure I have came up with in one day in bed, and this won't be a full series(I am yet a student, which means I don't have time to invent data structures all day and all night). Still, Thinking about this, I thought it would be a good idea to cover it on its own post. So here we are.

Concept

The traditional bit trie uses one leaf node for one number, and every leaf node has same depth. but about this, I thought — why? "Do we really have to use $$$32$$$ zeroes, just to represent a single zero? Heck no. There has to be a better way." And this is where I came up with this idea.

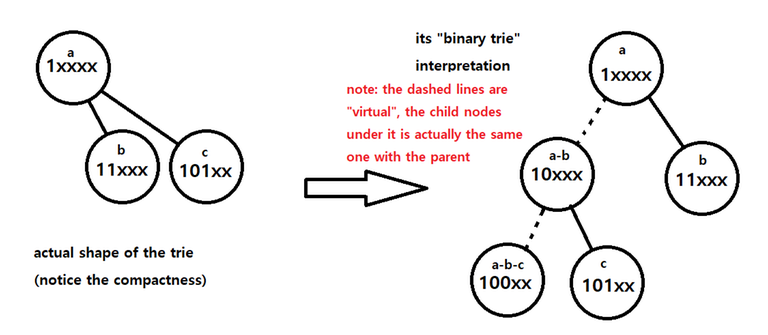
Instead of using the same old left-right child, let's use up to $$$l \leq depth$$$ children for one node. $$$l$$$ is the suffix part when each node represents a prefix. For every prefix node, we connect prefix nodes with only one $$$1$$$ bit determined after the current prefix. For example, under $$$1\text{xxxx}_2$$$, there are $$$11\text{xxx}_2$$$, $$$101\text{xx}_2$$$, and etc. Then, while the undetermined suffix (ex. the $$$\text{xxx}$$$ in $$$1\text{xxx}_2$$$) is, of course, undetermined, we can assume they are $$$0$$$ for the exact node the prefix exists on. Then we can use the prefix node $$$1\text{xxxx}_2$$$ for $$$10000_2$$$ also.

The Important Detail

At this moment, you should be wondering, how do we distinguish the node for the number $$$10000_2$$$ and the prefix $$$1\text{xxxx}_2$$$? They use the same node after all. My conclusion? You don't need to. To do this, you can just save the size (amount of elements) of the subtree. Now, let us denote the size of the subtree of prefix $$$S$$$ as $$$n(S)$$$. then $$$n(1\text{xxxx}_2) = n(11\text{xxx}_2) + n(101\text{xx}_2) + \ldots + n(10000_2)$$$ applies. So you can just traverse the child nodes one by one, and the rest is the number itself.

Traversing the Bit-indexed Trie

Using the "important detail" stated above, traversing the Bit-indexed Trie boils down to simply interpreting it like a binary tree. We start at the root, which is $$$0$$$, and we can interpret this node as $$$0\text{xxxxx}_2$$$. This root node may (or may not) have $$$01\text{xxxx}_2$$$ as a child node. Important point here is to keep a variable for the size of the "virtual" subtree of the current node. (we will denote this as $$$c$$$.) If the subtree size of the current node ($$$0\text{xxxxx}_2$$$) is $$$s$$$ and that of the right child node ($$$01\text{xxxx}_2$$$) is $$$s_1$$$, then the subtree size of the left child node, when interpreted as a binary trie, should be $$$s-s_1$$$. So if we want to traverse towards the right child node, do so, and update $$$c$$$ to $$$s_1$$$. On the other hand, if we want to traverse towards the left child node, stay on the current node, assume that we did move ($$$0\text{xxxxx}_2$$$ yet shares the node with $$$00\text{xxxx}_2$$$), and update $$$c$$$ to $$$c-s_1$$$. After understanding this, almost everything goes same with the usual trie.