Greedily take the smallest character in both strings. What's the exception to this?

We can't take the smallest character in both strings when we've already took $$$k$$$ elements from that string. Denote $$$A$$$ as the number of characters we've took from string $$$a$$$ in the last moves and denote $$$B$$$ the same for $$$b$$$. If $$$A=k$$$, then we have to take the smallest character in string $$$b$$$ instead of possibly $$$a$$$. If $$$B=k$$$, then we have to take the smallest charater in string $$$a$$$ instead of possibly $$$b$$$.

#include <bits/stdc++.h>
 
using namespace std;
 
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
 
    int t; cin>>t;
    while (t--)
    {
        int n,m,k; cin>>n>>m>>k;
        string a,b,c; cin>>a>>b;
        sort(a.begin(),a.end(),greater<char>());
        sort(b.begin(),b.end(),greater<char>());
 
        int ak=0,bk=0;
        while (!a.empty() && !b.empty())
        {
            bool gde=b.back()<a.back();
            if (gde && bk==k) gde=0;
            if (!gde && ak==k) gde=1;
 
            if (gde) c.push_back(b.back()),bk++,ak=0,b.pop_back();
            else c.push_back(a.back()),ak++,bk=0,a.pop_back();
        }
 
        cout<<c<<"\n";
    }
}

When is it impossible to find such permutation?

It is impossible only for $$$n=1$$$. In every other case, iterate over each position and take the smallest available number. What's the exception to this?

The exception is the last two elements. We can always take the smallest available number for each $$$q_i$$$ satisfying $$$i<n-1$$$. To do this we maintain an array of bools of already taken numbers, and then iterate over it to find the smallest available number satisfying $$$p_i\neq q_i$$$.

Now consider $$$(p_{n-1},p_{n})$$$ and we want $$$(q_{n-1},q_{n})$$$ to be lexicographically minimal. Let $$$a$$$ and $$$b$$$ be the last two unused numbers. It can be proven that at least one of the permutations ending with $$$(a,b)$$$ or $$$(b,a)$$$ will be valid. We just take the lexicographically minimal valid one.

#include <bits/stdc++.h>
 
using namespace std;
 
bool took[1005];
int p[1005];
 
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
 
    int t; cin>>t;
    while (t--)
    {
        int n; cin>>n;
        for (int i=1;i<=n;i++) cin>>p[i];
        for (int i=1;i<=n;i++) took[i]=0;
        
        if (n==1)
        {
            cout<<"-1\n";
            continue;
        }
 
        for (int i=1;i<=n-2;i++)
        {
            int k=1;
            while (took[k] || k==p[i]) ++k;
            cout<<k<<" "; took[k]=1;
        }
 
        int a=-1,b=-1;
        for (int i=1;i<=n;i++) if (!took[i])
        {
            if (a==-1) a=i;
            else b=i;
        }
 
        if (a!=p[n-1] && b!=p[n]) cout<<a<<" "<<b<<"\n";
        else cout<<b<<" "<<a<<"\n";
    }
}

#include <bits/stdc++.h>

using namespace std;

int t,n,A[1010],B[1010];

int main()
{
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(int i=1; i<=n; i++)
        {
            scanf("%d",&A[i]);
            B[i] = i;
        }
        if(n==1)
        {
            printf("-1\n");
            continue;
        }
        for(int i=1; i<n; i++)
        {
            if(A[i]==B[i]) swap(B[i],B[i+1]);
        }
        if(A[n]==B[n]) swap(B[n-1],B[n]);
        for(int i=1; i<=n; i++) printf("%d ",B[i]);
        printf("\n");
    }
    return 0;
}

We always delete a vertex directly connected to an infected one.

Use dp.

Let $$$u_1,u_2,...,u_k$$$ be the sequence of removed vertices such that the infection cannot spread anymore. If vertex $$$u_i$$$ was never directly connected to an infected vertex, then we could have deleted its parent instead of $$$u_i$$$ and we would get a better solution. Hence, we may assume we always delete a vertex directly connected to an infected one.

Now we may use some dynamic programming ideas. Let $$$dp_i$$$ be the maximum number of vertices we can save in the subtree of vertex $$$i$$$. If $$$c_1$$$ and $$$c_2$$$ are the children of vertex $$$i$$$, the transition is

where $$$s_i$$$ denotes the number of vertices in the subtree of $$$i$$$.

The answer to the problem is $$$dp_1$$$.

#include <bits/stdc++.h>
 
using namespace std;
 
vector<vector<int>> g(300005);
int ch[300005],dp[300005];
 
void dfs(int p, int q)
{
    ch[p]=1,dp[p]=0; int s=0;
    for (auto it : g[p]) if (it!=q)
    {
        dfs(it,p); s+=dp[it];
        ch[p]+=ch[it];
    }
    for (auto it : g[p]) if (it!=q)
    {
        dp[p]=max(dp[p],s-dp[it]+ch[it]-1);
    }
}
 
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
 
    int t; cin>>t;
    while (t--)
    {
        int n; cin>>n;
        for (int i=1;i<=n;i++) g[i].clear();
        for (int i=1;i<n;i++)
        {
            int u,v; cin>>u>>v;
            g[u].push_back(v);
            g[v].push_back(u);
        }
 
        dfs(1,0);
        cout<<dp[1]<<"\n";
    }
}

There are not a lot of useful black squares.

Consider this algorithm: iterate over all squares in the matrix and find the most distant black square.

Let's find out how to do that efficiently. In fact, only 4 (not necessarily distinct) squares will be useful: one square which minimizes $$$i-j$$$, one square which maximizes $$$i-j$$$, one square which minimizes $$$i+j$$$ and one square which maximizes $$$i+j$$$, where $$$(i,j)$$$ denotes the black cell's coordinates. In other words, we would like to find the most distant "border".

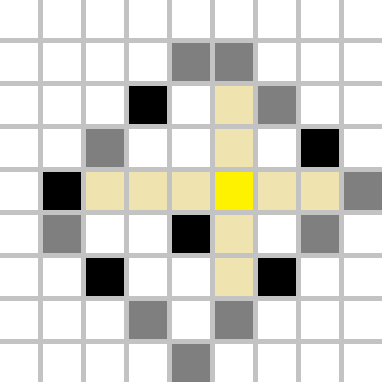
Let's look at the example above. The cell we choose to recolour to yellow creates four regions as shown. The most distant border will be fully contained inside one region, hence we should find distance from our yellow cell to any cell on that border, and that is the maximum possible distance.

#include <bits/stdc++.h>
 
using namespace std;
 
char tab[1003][1003];
pair<int,int> a={-1,-1},b={-1,-1},c={-1,-1},d={-1,-1};
 
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
 
    int t; cin>>t;
    while (t--)
    {
        a={-1,-1},b={-1,-1},c={-1,-1},d={-1,-1};
        
        int n,m; cin>>n>>m;
        for (int i=0;i<n;i++) cin>>tab[i];
 
        vector<pair<int,int>> interesting;
 
        for (int i=0;i<n;i++) for (int j=0;j<m;j++) if (tab[i][j]=='B')
        {
            if (a.first==-1 || i+j>a.first+a.second) a={i,j};
            if (b.first==-1 || i+j<b.first+b.second) b={i,j};
            if (c.first==-1 || i-j>c.first-c.second) c={i,j};
            if (d.first==-1 || i-j<d.first-d.second) d={i,j};
        }
 
        interesting.push_back(a);
        interesting.push_back(b);
        interesting.push_back(c);
        interesting.push_back(d);
 
        int ans=1e9; pair<int,int> opt;
        for (int i=0;i<n;i++) for (int j=0;j<m;j++)
        {
            int dist=0;
            for (auto it : interesting) dist=max(dist,abs(i-it.first)+abs(j-it.second));
            if (dist<ans) ans=dist,opt={i,j};
        }
 
        cout<<opt.first+1<<" "<<opt.second+1<<"\n";
    }
}