Hi all!
The 2018 ACM-ICPC Asia Shenyang Regional Contest has ended on October 21. At this site, 186 official teams and 6 guest teams selected from the preliminary online contest have competed in 5 hours, trying to solve 13 problems.
We are glad to invite you all from Codeforces, one of the greatest programming communities, to participate in its online-mirror contest, 2018-2019 ACM-ICPC, Asia Shenyang Regional Contest!
Please notice the online-mirror contest will start at an unusual time, Saturday, November 24, 2018 at 18:00 (UTC+8), when we are able to answer your questions during the online contest. By the way, we have added the onsite board, so when you are participating (during the mirror contest or virtual participation), you may take advantage of it!
This contest follows the ACM-ICPC rule and it will be unrated. Both personal registration and team registration are recommended. You may register for this contest 6 hours before it starts, but it is temporarily inaccessible before registration starts.
Also, many thanks to:
- Teachers, volunteers and technical staff from Northeastern University for holding such a wonderful contest;
- AHdoc, Claris, niike0goood, quailty and me for problem setting;
- yefllower, zscc, wangyenjen, adrien1018, eddy1021, waynetuinfor, boook, johnchen902, yp155136 and pr3pony for testing;
- MikeMirzayanov for Codeforces and Polygon platforms;
- icpc.foundation, JetBrains and Jisuanke for sponsoring the regional contest.
Besides, we kindly ask everybody who has already read the problems not to participate or discuss solutions in public before the contest has ended. Please keep the sportsmanship all the time!
Hope you enjoy the problems!
UPD1: Our sponsor Jisuanke will hold another online-mirror contest soon after the contest on Gym. If you missed this one, you could participate the other one, which will start on Sunday, November 25, 2018 at 12:00 (UTC+8) without the onsite board.
UPD2: Registration starts. You may view this page to register.
UPD3: Contest has ended. Any discussion will be greatly appreciated. If needed, we will discuss solutions after tomorrow.











I have practiced or participated onsite of 2018 Shenyang, 2018 Nanjing and 2018 Xuzhou Contests. From my perspective, I think Shenyang is typical of this year's ICPC East-Continent Regional contest for both problem structure and the onsite regional result. Can't wait to discuss about the problem after the mirror contest~
Thanks skywalkert, Claris, quailty along with other problem setters or testers for sharing this amazing contests in the community. and BTW, I believe it is unrated~~~
Thanks to the problem setter and tester, interesting contest.
Hi, how to solve K?
it seems that using only DP formula F(N,K) = (F(N-1, K) + K)%n is not enough...is there any critical observation?
Problem K is a typical Josephus problem, so its solution may be a well-known method.
Let the answer decreased by 1 as f(n, m, k). We could find the recurrence relation is that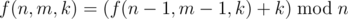 and
and 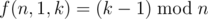 .
.
If m ≤ k, we can calculate f(n - m + 1, 1, k), f(n - m + 2, 2, k), ..., f(n, m, k) in order. The time complexity in this case is O(m).
If k ≤ m, we can find out that during the calculations from f(n - m + 1, 1, k) to f(n, m, k), there are many positions x satisfying f(n, x, k) = f(n - 1, x - 1, k) + k (i.e. the modulo operation doesn't affect at x). From the state f(n, x, k), we can find the minimum integer t such that f(n, x, k) + tk ≥ n + t and skip the states f(n', x', k) (x < x' < x + t). If k > 1, the "jump" process has at most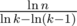 steps. (It may not be a tight upper bound, since it is just obtained from inequality scaling.) It is easy to show
steps. (It may not be a tight upper bound, since it is just obtained from inequality scaling.) It is easy to show 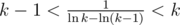 (using Cauchy's mean value theorem), so the time complexity in this case is
(using Cauchy's mean value theorem), so the time complexity in this case is  .
.
Actually, the time complexity of the skip method is . You can fix the case that k = 1 and use this skip method to get accepted.
. You can fix the case that k = 1 and use this skip method to get accepted.
How to solve A ?
I'm glad to see you trying to solve this problem. This problem can be solved in several ways, as the time limit is very loose. Here is the fastest way I could ever come up with.
Let the maximum depth be $$$H$$$. The number of nodes in the trie is $$$\mathcal{O}((n + m) H)$$$, but the number of useful nodes is only $$$\mathcal{O}(n + m)$$$. You can easily rebuild the tree for useful nodes.
Let's design a matching DP on the tree. In the DP state, we can either memorize the information in a subtree or the information on the path between the current node and the root. It's obvious that the latter is better, as $$$H$$$ is quite small.
So what's the state? Well, there are $$$5$$$ ways of matching: ($$$A \to B$$$ means that $$$A$$$ is an ancestor of $$$B$$$)
You may design a DP like $$$dp(u, c_1, c_2, c_3)$$$ where
The above DP may work in $$$\mathcal{O}((n + m) H^5)$$$, because of the transition $$$dp(u, p_1 + q_1, p_2 + q_2, p_3 + q_3) \gets dp(v_1, p_1, p_2, p_3) dp(v_2, q_1, q_2, q_3)$$$ for each node $$$u$$$ and its children nodes $$$u_1$$$, $$$u_2$$$. However, as the modulo number is a big prime number, it is not difficult to squeeze out $$$c_3$$$, and then the time complexity will become $$$\mathcal{O}((n + m) H^3)$$$. (The complexity analysis is left to readers :P)
Actually, the constant factor yielded in each solution is very small (e.g. $$$1 / 24$$$ or $$$1 / 120$$$), so it's not difficult to pass.
Thanks, i got it !
How to solve B? I know that if the range of the elements (l[i],r[i]) is small we can use FFT. But when it is large I don't know what to do.
Hint: For each position, there is at most one candidate with a high probability (greater than 0.5). If a matching occurs with a low probability (less than 1e-9), you can regard the probability as 0.
tls, How to solve problem M? I learned some dp trick in wanna-fly camp, but I still can't solve the entire problem. I would like a more specific editorial, please. Thanks very much.
Write down the generating function and you will find the solution.
In wanna-fly camp, Claris taught some tricks about this problem. Maybe you can solve this problem now if the problem becomes 01 backpack. Don't worry. You can solve it by understanding some of the knowledge about generating functions. A backpack for an item can be seen as $$$\sum_{i=0}^{a} x ^{bi} = \frac{1 - x ^{(a+1)b}}{1-x^b} $$$. First use (a+1)b to make a 01 backpack with a negative coefficient, and then divide by a x^b 01 backpack. Because $$$\sum_{i=0}^{\infty} x ^{bi} = \frac{1}{1-x^b} $$$, you can solve this division problem by doing a full backpack with a positive coefficient on x^b. About the deleted backpack,you can also solve by the way. $$$(1-x^b)*\sum_{i=0}^{\infty} x ^{i*(a+1)b} = \frac{1-x^b}{1 - x ^{(a+1)b}} $$$.The remaining questions (such as prefixes and the like) have already been mentioned by Claris. My English is poor, hope you can understand and then solve this interesting problem.
Could you explain more details about "First use (a+1)b to make a 01 backpack with a negative coefficient, and then divide by a x^b 01 backpack", do I need to use some polynomial algorithm or just like normal Knapsack problem? I learned some knowledge about generating function, but I don't know how to use them for this problem. Sorry for my low IQ. Thanks for the reply.
How to solve D?
It seemed to be a notorious coincidence: 1019E - Raining season (if we restrain all $$$a_i = 1$$$, then we get 101955D - Diameter of a Tree)
Though the tutorial for 1019E illustrated a solution running in $$$O(n \log^2 n + m)$$$, you can carefully modify that solution and make it run in $$$O(n \log n + m \log m)$$$ on 101955D.
The author's solution to 101955D is a bit complicated over data structure rather than geometry. To make it short, add some virtual vertices so that the degree of each vertex is at most 3, and then apply centroid decomposition and solve queries offline.
How to solve J ??? Its quite interesting...
Why this code Runtime error on test 2
K — Let the Flames Begin