Сегодня ночью закончился квалификационный раунд YTCF 2018. Хотелось бы обсудить задачи.

A: в задаче требовалось выбрать минимальное по размеру множество точек на прямой, от которых расстояние до остальных было бы не более R (от какой-либо из выбранных). В одномерном случае эта задача тривиальна, но мне интересно, существует ли какой-то эффективный алгоритм для двумерного случая?

B: стандартная одномерная динамика, нет особого смысла что-то по ней писать.

C: по условию вам даны две карты города — новая и старая — в следующем формате:

• множество ключевых точек, заданные двумя вещественными числами;
• улицы, являющиеся ломаными, построенными на ключевых точках.

Количество ключевых точек на карте N, количество улиц M и суммарное количество отрезков во всех улицах L₁ + L₂ + ... + L_m не превосходят 10⁴.

Целью задачи было определить, какие старые улицы находятся близко к каждой из новой. Старая улица располагалась близко к новой, если все её точки находились на расстоянии не более D от какой-либо точки ломаной, образующей новую улицу. (D также дано во входных данных).

Я не придумал ничего оптимальнее, чем решение за 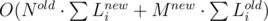— для каждой новой улицы проверить, находится ли к ней достаточно близко каждая из ключевых точек старой карты, а затем проверить условие для старой улицы как побитовое И всех ее ключевых точек. Грубая оценка подстановкой максимальных значений — 10⁸· константа · операции с вещественными числами, что ожидаемо не влезло в 1 секунду на Java 8.

Для этой задачи существует оптимальнее асимптотически решение? Или подобное можно было упихать на C++ (я не стал переписывать, хотя время было, так как оценка выше навевала уж слишком плохие мысли)?

D: дано N (1 ≤ N ≤ 300) точек на плоскости D_i — водители такси. Также дано N маршрутов, заданных точкой отправления P_j^start и точкой прибытия P_j^end. Расстояния в задаче считаются по манхэттенской метрике (|X₁ - X₂| + |Y₁ - Y₂|), длиной маршрута считалась сумма расстояний (D_i, P_j^start) и (P_j^start, P_j^end). Требовалось распределить водителей по маршрутам, чтобы минимизировать максимальную длину маршрута.

Я сдал бинарный поиск по ответу с проверкой совершенного паросочетания внутри. Является ли это стандартным решением для такого рода задач или существует какой-то способ оптимальнее?