Всем привет! Думаю, многие знают про такой тип данных, как множество. Он должен поддерживать следующие операции:

• Добавить элемент в множество;
• Узнать, есть ли элемент в множестве;
• Удалить элемент из множества.

Если речь идёт о множестве упорядоченном, то элементы также должны располагаться в нём в определённом порядке. Лично я считаю, что для упорядоченных множеств также очень важны следующие операции:

• Узнать, какой элемент является K-ым в множестве;
• Узнать, какой номер был бы у элемента, если бы он находился в этом множестве.

Чаще всего для реализации такого функционала используются двоичные сбалансированные деревья (AVL-дерево, красно-чёрное дерево, декартого дерево, etc). Однако в этой статье я бы хотел поговорить о некоторых особенностях в реализации упорядоченного множества на других структурах. В частности, в этой статье мною будут рассмотрены реализации на дереве Фенвика и на дереве отрезков. Сразу хочу отметить, что это позволяет воссоздать множество только над множеством натуральных чисел. Для любых прочих типов элементов в множестве такие методы не сработают :(

Основная идея такой схемы заключается в следующем:

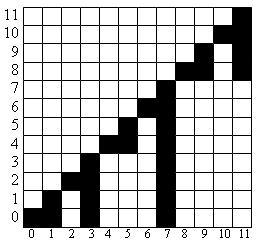Пускай индекс элемента в массиве (назовём его для удобства arr), над которым мы строим наше множество, будет соответствовать его значению, а значение — количеству таких элементов в множестве. Тогда легко заметить, что мы сможем выполнять все требуемые операции за время не хуже, чем логарифм, т.к. добавление элемента x в множество будет соответствовать инкрементированию ячейки arr[x] (или присвоению единицы, если множество уникальное), проверка элемента на наличие в множестве — это получение значения ячейки arr[x] (в дереве Фенвика не прокатит, там, судя по всему, прийдётся вычислить sum(x, x)), удаление элемента — декрементирование ячейки (присвоение 0, если множество уникальное), номер элемента в множестве — это sum(0, r - 1). Отдельно стоит отметить операцию нахождения K-ого элемента. Для этого прийдётся использовать технику двоичного подъёма. В дереве отрезков для этого потребуется поддерживать размеры поддеревьев, как в BST, а в дереве Фенвика мы можем, внимательно рассмотрев следующее изображение, показывающее принцип распределения элементов по частичным суммам, вывести такой алгоритм:

    int get(int x)
    {
        int sum=0;
        int ret=0; // Номер первого элемента в массиве, сумма в котором равна текущей
        for(int i=1<<MPOW;i && ret+(i-1)<N;i>>=1) // Перебираем степени двойки, начиная с максимально возможной
        {
            if(sum+arr[ret+(i-1)]<x) // Учитывая, что функция суммы монотонна, стараемся расширить текущий префикс
                sum+=arr[ret+(i-1)],
                ret+=i;
        }
        return ret;
    }

Легко заметить, что при таком подходе ret всегда имеет такое значение, что в следующий раз какое-то число из отрезка [0;ret] встретится не ранее, чем в точке ret+i, однако, в силу постояннного убывания i, мы никогда не достигнем такой точки, а значит, ни один элемент в префиксе не будет учтён дважды. Это даёт нам право полагать, что алгоритм правильный. И проверка на некоторых задачах это подтверждает :)

Основная идея изложена, теперь поговорим о достоинствах и недостатках такого подхода.

Достоинства:

• Быстро пишется;
• Интуитивно понятно (особенно, в случае с деревом отрезков);
• Быстро работает (на практике чаще всего обгоняет BST);

Недостатки:

• Ограниченная функциональность (поддерживает только натуральные числа в множестве);
• В самом простом виде занимает O(C) памяти, где C — максимальное возможное число в множестве;

Второй недостаток ОЧЕНЬ существенный. К счастью, его можно устранить. Сделать это можно двумя способами.

1. Сжатие координат. Если мы можем решать задачу в оффлайне, то мы считываем все запросы и узнаём все возможные индексы, к которым нам прийдётся обращаться. Сортируем их и ассоциируем с наименьшим из чисел единицу, со вторым — двойку и т.д. Это позволяет снизить расход памяти до O(M), где M — количество запросов. Однако, к сожалению, это не всегда работает.
2. Динамическое расширение дерева. Способ заключается в том, чтобы не хранить вершины в дереве, которые нам не нужны. Есть, как минимум, три способа. К сожалению, для дерева Фенвика подходит только один из них. Первый вариант — использовать хеш-мапы. Плохой, очень плохой вариант. Точнее, с ассимптотической точки зрения он хороший, но хеш-мапы обладают очень большими константами, поэтому я не рекомендую этот метод. К сожалению, именно он — тот единственный, что доступен для дерева Фенвика :). Второй — расширение указателями. Когда нам в дереве нужна новая вершина, мы просто создаём её. Дёшево и сердито. Однако, это всё ещё не самый быстрый вариант. Третий — статически выделить блок в MlogC вершин, после чего для каждой вершины хранить индексы её сыновей (как в боре). На практике именно этот способ оказывается наиболее быстрым. Расход памяти же во всех трёх способах снижается до O(MlogC), что уже, в целом, приемлемо.

Вновь надеюсь, что был интересен/полезен кому-нибудь. До новых встреч :)