| acmsguru |
|---|
| Закончено |
→ Теги задачи
Нет тегов
Нет прав на редактирование
Условие задачи было недавно изменено. Просмотреть изменения.
×
482. Impudent Thief
Time limit per test: 0.25 second(s)
Memory limit: 65536 kilobytes
Memory limit: 65536 kilobytes
input: standard
output: standard
output: standard
For most people Halloween evening is a time of having fun. But Mr. X chose the night after Halloween to commit a crime. He wants to get some boards to build a shed. And he decided to stole it from the fence of the neighbouring factory. But he wants to do it in such a way that nobody will notice boards loss. The fence consists of several boards with width, equal to 1, and integer heights (see picture). Mr. X is going to take some boards from the fence and then put the remaining boards together without changing their order to form a new fence. To be sure that noboby will notice the change, the perimeter of resulting fence should not be less than a half of the perimeter of initial fence. See picure description to understand the way of calculating fence's perimeter. With such constraint, Mr. X wants to maximize total height of extracted boards.
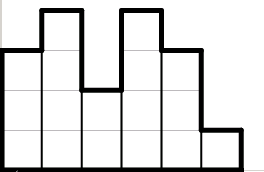
Perimeter of the fence is a perimeter of the figure, which is made by joining the rectangles corresponding to boards. For example, perimeter of the fence in the picture is marked bold and it's length is equal to 24.
Input
The first line contains integer number n (1 ≤ n ≤ 50) — number of boards in the fence. The second line contains n integer numbers hi — heights of the boards (1 ≤ hi ≤ 100). Boards are given from the leftmost one to the rightmost one.Output
In the first line output s — maximal total height of some subset of the boards, which can be taken without violating the described rule. In the second line output k — number of boards in such subset. In the third line output k numbers of the boards which should be stolen. Boards are numbered starting from 1 as they appear in the input. Print numbers in any order. If there are multiple solutions, output any.Example(s)
sample input | sample output |
6 3 4 2 4 3 1 | 12 4 1 3 4 5 |
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 20:23:00 (k1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|




