| acmsguru |
|---|
| Finished |
→ Problem tags
No tags yet
No tag edit access
The problem statement has recently been changed. View the changes.
×
469. Ghostbusters
Time limit per test: 0.5 second(s)
Memory limit: 262144 kilobytes
Memory limit: 262144 kilobytes
input: standard
output: standard
output: standard
Now famous Ghostbusters want your help. As you probably know, all ghosts that are caught are put in asylum to stay there forever (since they are already dead and cannot be obliterated). The problem is that though usually ghosts can intersect and even lie inside each other, some new ghosts by yet unknown to Egon reasons are afraid of some old ghosts and cannot intersect with them. That's what your problem is — to find the maximum radius of a new ghost that can be put to the asylum in the worst case (i.e., when it is afraid of all other ghosts in the asylum). You task is simplified by the fact that all ghosts are in fact perfect solid spheres and stay at the same points forever. Also don't forget that new ghost cannot intersect borders of the asylum (but can touch them as well as other ghosts).
Input
The first line of the input file contains three integer numbers W, H and D — sizes of the asylum given in meters (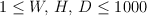 ). Asylum is a rectangular parallelepiped. Let us introduce coordinate system in such a way that two opposite corners of the asylum have coordinates (0,0,0) and (W,H,D). Then position of the i-th ghost can be described in this system as sphere centered at point with coordinates (Xi,Yi,Zi) and having radius Ri. Second line of the input file contains integer number N — number of ghosts in the asylum (0 ≤ N ≤ 10). i-th of the next N lines contains four numbers Xi, Yi, Zi and Ri (-1000 < Xi,Yi,Zi <2000, 0 ≤ Ri ≤ 1000). Though new ghost cannot intersect other ghosts and borders of the asylum, old ghosts may violate these rules and cross each other and boundaries of the asylum. However, it is guaranteed that at least some part of a ghost is contained inside the asylum. Ghost of radius 0 is supposed to consist of one point and cannot lie inside your ghost.
). Asylum is a rectangular parallelepiped. Let us introduce coordinate system in such a way that two opposite corners of the asylum have coordinates (0,0,0) and (W,H,D). Then position of the i-th ghost can be described in this system as sphere centered at point with coordinates (Xi,Yi,Zi) and having radius Ri. Second line of the input file contains integer number N — number of ghosts in the asylum (0 ≤ N ≤ 10). i-th of the next N lines contains four numbers Xi, Yi, Zi and Ri (-1000 < Xi,Yi,Zi <2000, 0 ≤ Ri ≤ 1000). Though new ghost cannot intersect other ghosts and borders of the asylum, old ghosts may violate these rules and cross each other and boundaries of the asylum. However, it is guaranteed that at least some part of a ghost is contained inside the asylum. Ghost of radius 0 is supposed to consist of one point and cannot lie inside your ghost.Output
To the output file write three numbers — coordinates of a point where ghost of required maximal radius, centered at this point, may stay. If there are several such points, output coordinates of any of them (but only one). Your output will be considered correct if maximal radius of a ghost centered at the point found by your program will be within 1 mm of the optimal one. To avoid any precision problems we recommend to output coordinates with maximal possible accuracy. It is guaranteed that at least one solution with positive radius will exist.Example(s)
sample input | sample output |
9 13 15 2 3 9 6 1 4 8 3 5 | 5 4 11 |
In the example, the first ghost is inside the second one. Ghost of maximum radius of 4 can stay at the point (5, 4, 11) — in this case it touches three borders of the asylum and the second ghost.
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/22/2024 18:33:02 (l2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




