| acmsguru |
|---|
| Закончено |
→ Теги задачи
Нет тегов
Нет прав на редактирование
Условие задачи было недавно изменено. Просмотреть изменения.
×
382. Cantor Function
Time limit per test: 0.25 second(s)
Memory limit: 262144 kilobytes
Memory limit: 262144 kilobytes
input: standard
output: standard
output: standard
The Cantor function f(x) (see picture) is defined as the function on [0, 1] as follows:
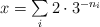 where ni are different positive integers), then
where ni are different positive integers), then 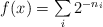 .
. In 2004, Gorin and Kukushkin showed that
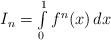 is rational. You are to find In and output it as irreducible fraction.
is rational. You are to find In and output it as irreducible fraction.Input
First line contains one integer number n (0 ≤ n ≤ 50).Output
You should output In in the form p/q, where p and q are the numerator and the denominator of In respectively. Note that p and q must be natural and (p, q) must be equal to 1. You should output p and q without leading zeroes.Example(s)
sample input | sample output |
0 | 1/1 |
sample input | sample output |
1 | 1/2 |
sample input | sample output |
2 | 3/10 |
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 00:38:20 (k2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|




