| acmsguru |
|---|
| Закончено |
→ Теги задачи
Нет тегов
Нет прав на редактирование
Условие задачи было недавно изменено. Просмотреть изменения.
×
380. Synchronised Alpinism
Time limit per test: 0.25 second(s)
Memory limit: 262144 kilobytes
Memory limit: 262144 kilobytes
input: standard
output: standard
output: standard
The progress does not stand! An institute of Sport Experiments (SE) is preparing new surprises for future Olympic Games. There is no doubt that you are familiar with synchronised swimming. But do you know anything about synchronised boxing or synchronised basketball? In this problem we will consider only synchronised alpinism. It is a team competition, each team consists of two members. Initially one of them stands at the east side of the mountain and other — at the west side. Their aim is to meet at some point as fast as possible. There is also one additional difficulty: at any moment of time they have to be at the same height. Unfortunatly, SE's synchronised alpinism experimental contest was unsuccessful. No team managed to fulfill the task, so it was impossible to determine a winner! Now SE is interested, is it really impossible to meet on the mountain under above restrictions or the teams just have to train harder. Try to help SE!
Input
Here we will assume that mountain is flat figure, and its border is a polyline, with a peaks at points (1, y1),..., (n, yn). The first line of the input file consists one integer number n (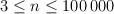 ). The second line contains integer numbers y1,..., yn. Points (1, y1) and (n, yn) are initial positions of alpinists. It is guaranteed that y1=0, yn=0 and y1,..., yn do not exceed
). The second line contains integer numbers y1,..., yn. Points (1, y1) and (n, yn) are initial positions of alpinists. It is guaranteed that y1=0, yn=0 and y1,..., yn do not exceed 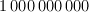 by absolute value.
by absolute value. Output
If it is possible for the alpinists to meet, output "YES", otherwise output "
NO" (quotes for clarity).
Example(s)
sample input | sample output |
7 0 3 1 5 2 4 0 | YES |
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 26.11.2024 12:14:24 (k3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|




