| Codeforces Round 485 (Div. 1) |
|---|
| Закончено |
→ Виртуальное участие
Виртуальное соревнование – это способ прорешать прошедшее соревнование в режиме, максимально близком к участию во время его проведения. Поддерживается только ICPC режим для виртуальных соревнований.
Если вы раньше видели эти задачи,
виртуальное соревнование не для вас – решайте эти задачи в архиве.
Если вы хотите просто дорешать задачи, виртуальное соревнование не для вас – решайте эти задачи в архиве.
Запрещается использовать чужой код, читать разборы задач и общаться по содержанию соревнования с кем-либо.
→ Теги задачи
битмаски
графы
поиск в глубину и подобное
снм
*2500
Нет прав на редактирование
→ Материалы соревнования
Условие задачи было недавно изменено. Просмотреть изменения.
×
C. AND Graph
ограничение по времени на тест
4 секундыограничение по памяти на тест
256 мегабайтввод
стандартный вводвывод
стандартный выводДано множество размера $$$m$$$, состоящее из целых неотрицательных чисел от $$$0$$$ до $$$2^{n}-1$$$ включительно. Построим на этих числах неориентированный граф следующим образом: соединим $$$x$$$ и $$$y$$$, если и только если $$$x \& y = 0$$$. Здесь $$$\&$$$ — операция побитового И. Посчитайте количество компонент связности в таком графе.
Входные данные
В первой строке записаны два целых числа $$$n$$$ и $$$m$$$ ($$$0 \le n \le 22$$$, $$$1 \le m \le 2^{n}$$$).
Во второй строке через пробел перечислены $$$m$$$ чисел $$$a_1, a_2, \ldots, a_m$$$ ($$$0 \le a_{i} < 2^{n}$$$) — элементы множества. Все $$$a_{i}$$$ различны.
Выходные данные
Выведите одно целое число — количество компонент связности.
Примеры
Входные данные
2 3
1 2 3
Выходные данные
2
Входные данные
5 5
5 19 10 20 12
Выходные данные
2
Примечание
Граф из первого примера:
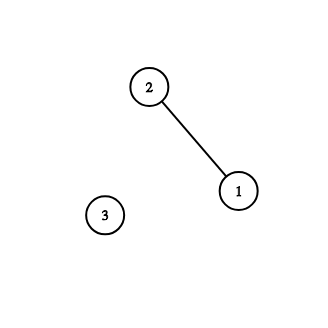
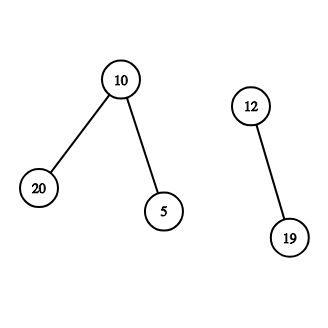
Граф из второго примера:
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 00:06:25 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|




