| Codeforces Round 480 (Div. 2) |
|---|
| Закончено |
Вам дан специальный связный неориентированный граф, в котором каждая вершина принадлежит максимум к одному простому циклу.
Ваша задача — убрать из этого графа столько рёбер, сколько необходимо, чтобы превратить этот граф в дерево (связный граф без циклов).
Для каждой вершины независимо выведите максимальное расстояние от неё до листа в результирующем дереве, предполагая, что рёбра были убраны так, чтобы минимизировать данное расстояние.
В первой строке ввода содержится два целых числа $$$n$$$ и $$$m$$$ ($$$1 \leq n \leq 5\cdot 10^5$$$) — число вершин и рёбер в изначальном графе соответственно.
В каждой из следующих $$$m$$$ строк содержится по два целых числа $$$u$$$ and $$$v$$$ ($$$1 \leq u,v \leq n$$$, $$$u \ne v$$$), означающих, что в графе есть ребро, соединяющее вершины $$$u$$$ и $$$v$$$. Каждая пара вершин соединена максимум одним ребром.
Гарантируется, что данный вам граф связен и каждая вершина в нём принадлежит максимум к одному простому циклу.
Выведите $$$n$$$ целых чисел, разделённых пробелами, $$$i$$$-е из которых обозначает максимальное расстояние между вершиной $$$i$$$ и листом дерева, если убранные рёбра были выбраны таким образом, что это расстояние минимально среди всех возможных вариантов убирания рёбер.
9 10
7 2
9 2
1 6
3 1
4 3
4 7
7 6
9 8
5 8
5 9
5 3 5 4 5 4 3 5 4
4 4
1 2
2 3
3 4
4 1
2 2 2 2
В первом примере один из возможных путей минимизации максимального расстояния от вершины $$$1$$$ — убирание отмеченных на следующем изображении рёбер:
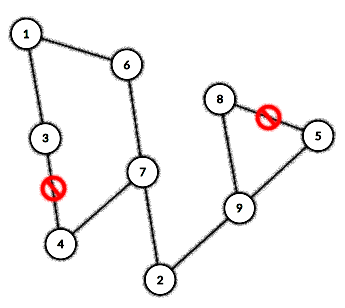
Обратите внимание, что для минимизации ответа для разных вершин можно убирать разные ребра.
| Название |
|---|




