Прямоугольник со сторонами $$$A$$$ и $$$B$$$ разрезали на прямоугольники разрезами, параллельными его сторонам. Например, если было сделано $$$p$$$ горизонтальных и $$$q$$$ вертикальных разрезов, то было получено $$$(p + 1) \cdot (q + 1)$$$ прямоугольников. В результате было получено $$$n$$$ различных видов прямоугольников. Два прямоугольника различны, если хотя бы одна сторона у них имеет разную длину. Обратите внимание, что прямоугольники не поворачивали, то есть прямоугольники $$$a \times b$$$ и $$$b \times a$$$ считаются различными при $$$a \neq b$$$.
Для каждого вида прямоуольников даны размеры прямоугольников этого вида, а также количество прямоугольников этого вида, которое было получено в результате разреза исходного прямоугольника.
Посчитайте количество пар $$$(A; B)$$$ таких, что в результате разрезания прямоугольника со сторонами $$$A$$$ и $$$B$$$ могли быть получены данные прямоугольники. Обратите внимание, что $$$(A; B)$$$ и $$$(B; A)$$$ считаются различными парами при $$$A \neq B$$$.
В первой строке находится целое число $$$n$$$ ($$$1 \leq n \leq 2 \cdot 10^{5}$$$) — количество видов прямоугольников, полученных в результате разрезания исходного прямоугольника.
В следующих $$$n$$$ строках содержатся три целых числа $$$w_{i}, h_{i}, c_{i}$$$ $$$(1 \leq w_{i}, h_{i}, c_{i} \leq 10^{12})$$$ — размеры прямоугольника некоторого вида и количество прямоугольников такого вида.
Гарантируется, что прямоугольники разных видов различны.
Выведите одно целое число — ответ на задачу.
1
1 1 9
3
2
2 3 20
2 4 40
6
2
1 2 5
2 3 5
0
В первом примере подходящими парами являются $$$(1; 9)$$$, $$$(3; 3)$$$ и $$$(9; 1)$$$.
Во втором примере есть 6 подходящих пар: $$$(2; 220)$$$, $$$(4; 110)$$$, $$$(8; 55)$$$, $$$(10; 44)$$$, $$$(20; 22)$$$ и $$$(40; 11)$$$.
Ниже пример разрезания для получения $$$(20; 22)$$$.
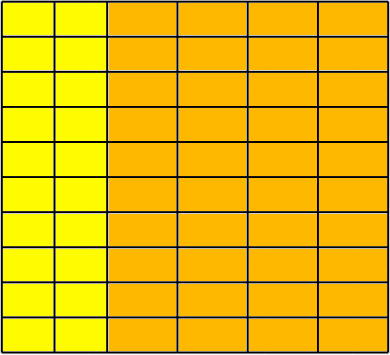
В третьем примере не существует ни одной подходящей пары.
| Название |
|---|




