У Пети есть многоугольник, состоящий из $$$n$$$ вершин.
Все стороны многоугольника Пети параллельны осям координат, а каждые две смежные стороны многоугольника Пети — перпендикулярны. Гарантируется, что многоугольник простой, то есть не имеет самопересечений и самокасаний. Вся внутренняя часть (границы не учитываются) многоугольника была покрашена Петей в черный цвет.
Также у Пети есть прямоугольное окно, заданное своими координатами, через которое он смотрит на свой многоугольник. Прямоугольное окно задается своими координатами и не может быть перемещено. Стороны прямоугольного окна параллельны осям координат.
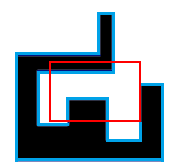Синим цветом изображена граница многоугольника, красным — окно. Ответ в этом случае равен 2. Определите количество черных связных областей многоугольника Пети, которые можно увидеть через прямоугольное окно.
В первой строке следуют четыре целых числа $$$x_1, y_1, x_2, y_2$$$ ($$$x_1 < x_2$$$, $$$y_2 < y_1$$$) — координаты левого верхнего и правого нижнего углов прямоугольного окна.
Во второй строке следует целое число $$$n$$$ ($$$4 \le n \le 15\,000$$$) — количество вершин в многоугольнике Пети.
В каждой из следующих $$$n$$$ строк следуют по два целых числа — координаты вершин многоугольника Пети в порядке обхода против часовой стрелки. Гарантируется, что заданный многоугольник удовлетворяет условию.
Значения всех координат прямоугольного окна и всех координат многоугольника неотрицательны и не превосходят $$$15\,000$$$.
Выведите количество черных связных областей многоугольника Пети, которые можно увидеть через прямоугольное окно.
5 7 16 3
16
0 0
18 0
18 6
16 6
16 1
10 1
10 4
7 4
7 2
2 2
2 6
12 6
12 12
10 12
10 8
0 8
2
Пример из условия соответствует картинке выше.
