You are given a string s consisting of n lowercase Latin letters.
Let's denote k-substring of s as a string subsk = sksk + 1..sn + 1 - k. Obviously, subs1 = s, and there are exactly 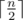 such substrings.
such substrings.
Let's call some string t an odd proper suprefix of a string T iff the following conditions are met:
- |T| > |t|;
- |t| is an odd number;
- t is simultaneously a prefix and a suffix of T.
For evey k-substring (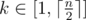 ) of s you have to calculate the maximum length of its odd proper suprefix.
) of s you have to calculate the maximum length of its odd proper suprefix.
The first line contains one integer n (2 ≤ n ≤ 106) — the length s.
The second line contains the string s consisting of n lowercase Latin letters.
Print 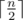 integers. i-th of them should be equal to maximum length of an odd proper suprefix of i-substring of s (or - 1, if there is no such string that is an odd proper suprefix of i-substring).
integers. i-th of them should be equal to maximum length of an odd proper suprefix of i-substring of s (or - 1, if there is no such string that is an odd proper suprefix of i-substring).
15
bcabcabcabcabca
9 7 5 3 1 -1 -1 -1
24
abaaabaaaabaaabaaaabaaab
15 13 11 9 7 5 3 1 1 -1 -1 1
19
cabcabbcabcabbcabca
5 3 1 -1 -1 1 1 -1 -1 -1
The answer for first sample test is folowing:
- 1-substring: bcabcabcabcabca
- 2-substring: cabcabcabcabc
- 3-substring: abcabcabcab
- 4-substring: bcabcabca
- 5-substring: cabcabc
- 6-substring: abcab
- 7-substring: bca
- 8-substring: c
| Name |
|---|




