Есть матрица A размера x × y, состоящая из целых чисел. Для каждого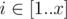 
, 
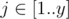Ai, j = y(i - 1) + j. Очевидно, каждое целое число из [1..xy] встречается в матрице ровно один раз.
Вы прошли по какому-то пути в этой матрице. Путь может быть описан последовательностью посещенных ячеек a1, a2, ..., an, обозначающей, что вы начали в ячейке, содержащей число a1, затем перешли в ячейку с числом a2 и так далее.
Из клетки в i-й строке и j-м столбце (определим ее как (i, j)) можно перейти в следующие ячейки:
- (i + 1, j) — если i < x;
- (i, j + 1) — если j < y;
- (i - 1, j) — если i > 1;
- (i, j - 1) — если j > 1.
Заметьте, что один шаг требует перехода в соседнюю ячейку. Остаться в той же ячейке не разрешается.
Значения x и y не известны заранее, вам необходимо найти любые из возможных значений этих чисел такие, что можно начать в клетке, содержащей a1, потом перейти в клетку, содержащую a2 (за один ход), потом в ячейку с a3 (также за один ход) и так далее. Можно ли выбрать значения x и y так, чтобы последовательность шагов была корректной.
В первой строке записано одно целое число n (1 ≤ n ≤ 200000) — количество клеток, которые вы посетили на пути (если какая-то клетка посещена дважды, то она и записана дважды).
Во второй строке записаны n чисел a1, a2, ..., an (1 ≤ ai ≤ 109) — числа на ячейках на вашем пути.
Если не существует значений x и y таких, что 1 ≤ x, y ≤ 109 и информация о пути корректна, то выведите NO.
В противном случае выведите YES в первой строке, а во второй — значения x и y такие, что путь корректен с данным числом строк и столбцов в матрице. Помните, что это должны быть целые положительные числа, не превышающие 109.
8
1 2 3 6 9 8 5 2
YES
3 3
6
1 2 1 2 5 3
NO
2
1 10
YES
4 9
Матрица и путь в ней в первом примере выглядит так:
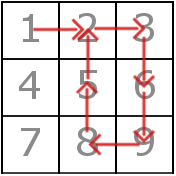
Существует несколько правильных ответов для первого и третьего примеров.
