Участники популярной музыкальной группы «Flayer» объявили о своем прощальном мировом турне. Разумеется, посетят они и Берляндию.
В Берляндии n городов. Между городами можно перемещаться, используя двусторонние железнодорожные маршруты; есть ровно m маршрутов, i-й используется для поездки из города vi в город ui (и из ui в vi) и стоит wi монет.
«Flayer» посетят все города, в i-м городе цена билета на концерт составит ai монет.
У вас есть друзья в каждом городе Берляндии, и все знают о ваших программистских способностях! Они просят вас посчитать, за какое минимальное количество монет им удастся посетить концерт. Для каждого города i необходимо посчитать минимальное количество монет, которое придется потратить жителю города i, чтобы доехать до какого-либо города j (или остаться в городе i), посетить там концерт, и вернуться в город i (если j ≠ i).
Формально, для каждого 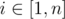 требуется посчитать
требуется посчитать 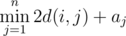 , где d(i, j) — минимальное количество монет, нужных для поездки из города i в город j. Если невозможно приехать в город j из города i, то d(i, j) считается бесконечно большим.
, где d(i, j) — минимальное количество монет, нужных для поездки из города i в город j. Если невозможно приехать в город j из города i, то d(i, j) считается бесконечно большим.
В первой строке записано два целых числа n и m (2 ≤ n ≤ 2·105, 1 ≤ m ≤ 2·105).
Затем идет m строк, в i-й записаны три целых числа vi, ui и wi (1 ≤ vi, ui ≤ n, vi ≠ ui, 1 ≤ wi ≤ 1012), определяющие i-й железнодорожный маршрут. Между каждой парой городов существует не больше одного железнодорожного маршрута, то есть, для каждой пары (v, u) во входных данных нет ни (u, v), ни дополнительных вхождений (v, u).
В следующей строке записаны n целых чисел a1, a2, ... ak (1 ≤ ai ≤ 1012) — цена билета на концерт в городе i.
Выведите n целых чисел. i-е из них должно быть равно минимальному количеству монет, которое придется потратить жителю города i для того, чтобы доехать до какого-либо города j (или остаться в городе i), посетить там концерт, и вернуться в город i (если j ≠ i).
4 2
1 2 4
2 3 7
6 20 1 25
6 14 1 25
3 3
1 2 1
2 3 1
1 3 1
30 10 20
12 10 12
| Название |
|---|




