| VK Cup 2018 - Раунд 2 |
|---|
| Закончено |
Атом вещества X может находиться в n различных состояниях с энергиями E1 < E2 < ... < En. Аркадий хочет построить лазер на этом веществе по трехуровневой схеме. Опишем упрощенно эту схему.
Выбираются три различных состояния атома i, j и k, где i < j < k. Затем происходит следующий процесс:
- изначально атом находится в состоянии i,
- затрачивается энергия Ek - Ei для перевода атома в состояние k,
- атом испускает фотон с полезной энергией Ek - Ej и переходит в состояние j,
- атом самопроизвольно переходит в состояние i, теряя энергию Ej - Ei,
- процесс повторяется с пункта 1.
Коэффициентом полезного действия (КПД) процесса назовем величину 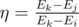 , то есть отношение полезной энергии фотона к затраченной энергии.
, то есть отношение полезной энергии фотона к затраченной энергии.
Из-за некоторых ограничений Аркадий может выбрать лишь такие три состояния, для которых Ek - Ei ≤ U.
Помогите Аркадию найти максимально возможный КПД процесса среди таких вариантов.
В первой строке следуют два целых числа n и U (3 ≤ n ≤ 105, 1 ≤ U ≤ 109) — количество состояний и максимальная допустимая разность между Ek и Ei.
Во второй строке следует последовательность целых чисел E1, E2, ..., En (1 ≤ E1 < E2... < En ≤ 109). Гарантируется, что все Ei заданы в порядке возрастания.
Если не существует ни одного способа для выбора состояний, выведите -1.
В противном случае выведите одно вещественное число η — максимально возможный КПД.
Ваш ответ будет зачтен, если его относительная или абсолютная погрешность не превосходит 10 - 9.
Формально, пусть ваш ответ равен a, а ответ жюри равен b. Ваш ответ будет зачтен, если 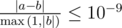 .
.
4 4
1 3 5 7
0.5
10 8
10 13 15 16 17 19 20 22 24 25
0.875
3 1
2 5 10
-1
В первом примере можно выбрать уровни 1, 2 и 3. В этом случае КПД равен 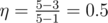 .
.
Во втором примере можно выбрать уровни 4, 5 и 9. В этом случае КПД равен 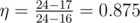 .
.
| Название |
|---|




