A. Полив
ограничение по времени на тест
1 секунда
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Зимой Максим решил наконец-то заняться тем, про что постоянно напоминала ему мама — поливкой огорода.

Огород представляет собой n грядок, пронумерованных от 1 до n. На k грядках огорода расположены краны (i-й кран — на грядке xi), которые при включении начинают распространять воду на соседние грядки. Если кран на грядке xi включён, то через одну секунду будет полита грядка xi, через две — грядки с отрезка [xi - 1, xi + 1] (если они существуют), через j (j — целое число) — с отрезка [xi - (j - 1), xi + (j - 1)] (если они существуют). В течение секунды ничего не меняется, то есть нельзя сказать, что отрезок [xi - 2.5, xi + 2.5] будет полит через 2.5 секунды; в этот момент будет полит только отрезок [xi - 2, xi + 2].

Огород из 1 теста. Белый цвет обозначает грядку без крана, красный — грядку с краном.
Огород из 1 теста через 2 секунды после включения крана. Белый цвет обозначает грядку, которая не полита, голубой — политую грядку.

Максим хочет узнать, за какое минимальное количество времени, если он одновременно включит все краны, весь огород будет полит. Помогите ему с этим!

Входные данные

В первой строке входных данных задано одно число t (1 ≤ t ≤ 200) — количество наборов тестовых данных, для которых нужно решить задачу.

Затем следуют t наборов. Первая строка набора содержит два целых числа n и k (1 ≤ n ≤ 200, 1 ≤ k ≤ n) — количество грядок и кранов, соответственно.

Следующая строка набора содержит k целых чисел xi (1 ≤ xi ≤ n) — грядка, в которой установлен i-й кран. Гарантируется, что для любого 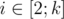выполняется xi - 1 < xi.

Гарантируется, что сумма n по всем наборам не превосходит 200.

Обратите внимание, во взломах можно использовать только t = 1.

Выходные данные

Для каждого набора выведите единственное целое число — через какое минимальное время Максим сможет полить весь огород.

Пример
Входные данные
3
5 1
3
3 3
1 2 3
4 1
1
Выходные данные
3
1
4
Примечание

Разбор примера из условия. В нём 3 набора тестовых данных:

  1. Огород из 5 грядок, в грядке под номером 3 кран. Если его включить, через 1 секунду грядка 3 будет полита; через 2 секунды грядки [1, 3] будет политы, и через 3 секунды всё будет полито.
  2. 3 грядки, кран в каждой из них. Если включить все краны, то всё будет полито через 1 секунду.
  3. 4 грядки, и один кран в грядке 1. Потребуется 4 секунды, чтобы полить, к примеру, грядку 4.