| Codeforces Round 457 (Div. 2) |
|---|
| Закончено |
Джейми готовит раунд на Codeforces. Он придумал задачу, но не знает, как её решить. Помогите ему решить следующую задачу:
Найдите k целых чисел таких, что суммы степеней двойки с такими показателями равны n и наибольшее число среди них минимально. Так как ответ может быть не единственен, найдите лексикографически максимальный ответ.
Более формально, рассмотрим все последовательности целых чисел длины k (a1, a2, ..., ak) такие, что 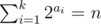 . Для каждой последовательности вычислим
. Для каждой последовательности вычислим 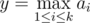 . Среди всех последовательностей с минимальным y выведите лексикографически наибольшую.
. Среди всех последовательностей с минимальным y выведите лексикографически наибольшую.
Определения степеней двойки и лексикографического порядка смотрите в примечаниях.
В первой строке содержатся два целых числа n и k (1 ≤ n ≤ 1018, 1 ≤ k ≤ 105) — требуемая сумма и длина последовательности.
Выведите «No» (без кавычек), если требуемой последовательности не существует. Иначе выведите в первой строке «Yes» (без кавычек), а во второй строке k чисел через пробел — элементы последовательности.
Гарантируется, что числа в ответе принадлежат отрезку [ - 1018, 1018].
23 5
Yes
3 3 2 1 0
13 2
No
1 2
Yes
-1 -1
В первом тестовом примере:
23 + 23 + 22 + 21 + 20 = 8 + 8 + 4 + 2 + 1 = 23
Последовательности (3, 3, 2, 0, 1) и (0, 1, 2, 3, 3) не являются правильным ответом, так как правильный ответ лексикографически больше, чем каждая из них.
Последовательность (4, 1, 1, 1, 0) не является правильным ответом, так как в правильном ответе значение y меньше.
Во втором тестовом примере можно показать, что требуемой последовательности не существует.
В третьем тестовом примере 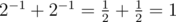 .
.
По определению:
Если x > 0, то 2x = 2·2·2·...·2 (x раз).
Если x = 0, то 2x = 1.
Если x < 0, то 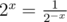 .
.
Лекксикографический порядок:
Для двух последовательностей одинаковой длины (a1, a2, ... , ak) и (b1, b2, ... , bk) первая последовательность лексикографически меньше второй тогда и только тогда когда, ai < bi, для первого i такого, что ai и bi различаются.
| Название |
|---|




