| Good Bye 2017 |
|---|
| Закончено |
Вам дано целое число m.
Пусть M = 2m - 1.
Вам дано множество из n целых чисел, обозначим его за T. Эти целые числа будут даны в двоичной системе счисления как n бинарных строк длины m.
Множество целых чисел S называется «хорошим», если следующие условия выполняются.
- Если
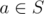 , то
, то 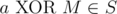 .
. - Если
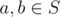 , то
, то 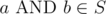
-
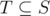
- Все элементы S меньше либо равны M.
Здесь 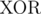 и
и 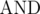 обозначают побитовые операции исключающее ИЛИ и И, соответственно.
обозначают побитовые операции исключающее ИЛИ и И, соответственно.
Вычислите количество хороших множеств S по модулю 109 + 7.
Первая строка содержит два целых числа m и n (1 ≤ m ≤ 1 000, 1 ≤ n ≤ min(2m, 50)).
Следующие n строк содержат элементы T. Каждая строка содержит ровно одну строку длины m из нулей и единиц. Все элементы T различны.
Выведите одно число: количество хороших множеств по модулю 109 + 7.
5 3
11010
00101
11000
4
30 2
010101010101010010101010101010
110110110110110011011011011011
860616440
Пример хорошего множества S: {00000, 00101, 00010, 00111, 11000, 11010, 11101, 11111}.
| Название |
|---|




