| Good Bye 2017 |
|---|
| Finished |
→ Virtual participation
Virtual contest is a way to take part in past contest, as close as possible to participation on time. It is supported only ICPC mode for virtual contests.
If you've seen these problems, a virtual contest is not for you - solve these problems in the archive.
If you just want to solve some problem from a contest, a virtual contest is not for you - solve this problem in the archive.
Never use someone else's code, read the tutorials or communicate with other person during a virtual contest.
→ Problem tags
bitmasks
combinatorics
dp
math
*2500
No tag edit access
→ Contest materials
The problem statement has recently been changed. View the changes.
×
E. New Year and Entity Enumeration
time limit per test
2 secondsmemory limit per test
256 megabytesinput
standard inputoutput
standard outputYou are given an integer m.
Let M = 2m - 1.
You are also given a set of n integers denoted as the set T. The integers will be provided in base 2 as n binary strings of length m.
A set of integers S is called "good" if the following hold.
- If
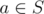 , then
, then 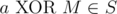 .
. - If
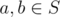 , then
, then 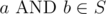
-
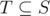
- All elements of S are less than or equal to M.
Here, 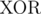 and
and 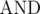 refer to the bitwise XOR and bitwise AND operators, respectively.
refer to the bitwise XOR and bitwise AND operators, respectively.
Count the number of good sets S, modulo 109 + 7.
Input
The first line will contain two integers m and n (1 ≤ m ≤ 1 000, 1 ≤ n ≤ min(2m, 50)).
The next n lines will contain the elements of T. Each line will contain exactly m zeros and ones. Elements of T will be distinct.
Output
Print a single integer, the number of good sets modulo 109 + 7.
Examples
Input
5 3
11010
00101
11000
Output
4
Input
30 2
010101010101010010101010101010
110110110110110011011011011011
Output
860616440
Note
An example of a valid set S is {00000, 00101, 00010, 00111, 11000, 11010, 11101, 11111}.
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/25/2025 12:38:03 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




