| Good Bye 2017 |
|---|
| Закончено |
Кэрол играет в керлинг.
У нее есть n дисков радиуса r на плоскости.
Изначально все диски находятся выше линии y = 10100.
Кэрол пускает диски по направлению к прямой y = 0 по одному в порядке от 1 до n.
Когда она пускает i-й диск, она ставит его центр в точку (xi, 10100), а затем толкает его так, что его y координата начинает уменьшаться, а координата x остается постоянной. Диск останавливается, когда он касается прямой y = 0 или любого предыдущего диска. Обратите внимание, как только диск остановился, он больше не двигается, даже от удара следующих дисков.
Вычислите координату y центров всех дисков после того, как они остановятся.
Первая строка содержит два целых числа n и r (1 ≤ n, r ≤ 1 000) — количество дисков и радиус каждого диска, соответственно.
Следующая строка содержит n целых чисел x1, x2, ..., xn (1 ≤ xi ≤ 1 000) — x-координаты дисков.
Выведите единственную строку с n числами. i-е из этих чисел должно быть равно итоговой y-координате центра i-го диска. Ваш ответ будет зачтен, если его абсолютная или относительная ошибка не превосходит 10 - 6.
А именно, пусть ваш ответ для определенного диска равен a, а ответ жюри — b. Ваш ответ будет зачтен, если 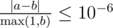 для всех дисков.
для всех дисков.
6 2
5 5 6 8 3 12
2 6.0 9.87298334621 13.3370849613 12.5187346573 13.3370849613
В первом примере конечные позиции дисков показаны на рисунке:
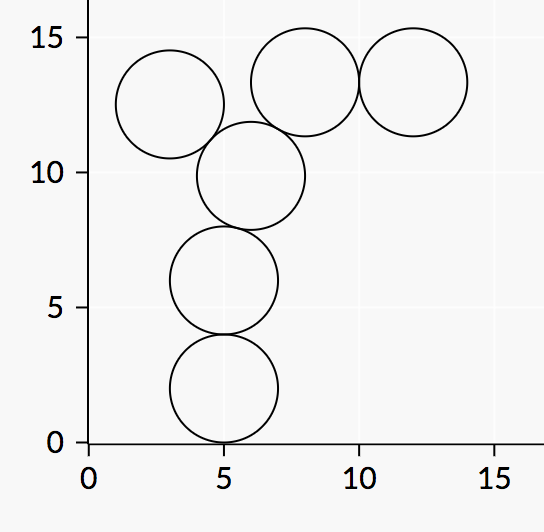
В частности, обратите внимание на положение последнего диска.
| Название |
|---|




