В этой задаче вам придётся иметь дело с очень специфичной ориентированной сетью (взвешенным ориентированным графом).
Сеть состоит из двух частей: части A и части B. Каждая часть состоит из n вершин; i-ю вершину части A будем обозначать как Ai, а i-ю вершину части B — как Bi.
Для каждого i (1 ≤ i < n) существует ориентированное ребро из Ai в Ai + 1, а также из Bi в Bi + 1. Пропускные способности этих рёбер заданы во входных данных. Также может быть несколько рёбер, ведущих из A в B (но нет таких рёбер, которые ведут из B в A).
Вам необходимо посчитать величину максимального потока из A1 в Bn в данной сети. Пропускные способности рёбер, ведущих из Ai в Ai + 1, также могут иногда меняться, и вам нужно пересчитывать величину потока после этих изменений. Вся остальная часть сети фиксирована (не происходит никаких изменений в части B, никаких изменений рёбер, ведущих из A в B, никакие рёбра не добавляются и не удаляются).
Посмотрите на пример и пояснение к нему, чтобы лучше понять структуру сети.
В первой строке записаны три числа n, m и q (2 ≤ n, m ≤ 2·105, 0 ≤ q ≤ 2·105) — количество вершин в каждой части, количество рёбер, ведущих из A в B, и количество изменений соответственно.
Далее следуют n - 1 строк. В i-й строке записаны два числа xi и yi, обозначающих, что ребро из Ai в Ai + 1 имеет пропускную способность xi, а ребро из Bi в Bi + 1 имеет пропускную способность yi (1 ≤ xi, yi ≤ 109).
В следующих m строках указываются рёбра из A в B. Каждая строка содержит три целых числа x, y и z, обозначающих ребро из Ax в By с пропускной способностью z (1 ≤ x, y ≤ n, 1 ≤ z ≤ 109). Может быть несколько рёбер, ведущих из Ax в By.
В последних q строках обозначаются изменения, вносимые в сеть. В i-й из этих строк записаны два числа vi и wi, обозначающих, что пропускная способность ребра из Avi в Avi + 1 становится равной wi (1 ≤ vi < n, 1 ≤ wi ≤ 109).
Сначала выведите величину максимального потока в исходной сети. Затем выведите q чисел, i-е из которых должно быть равно величине максимального потока после i-го изменения.
4 3 2
1 2
3 4
5 6
2 2 7
1 4 8
4 3 9
1 100
2 100
9
14
14
В примере до всех изменений сеть выглядит так:
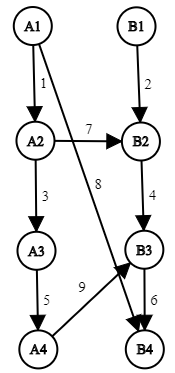
| Название |
|---|




