| Яндекс.Алгоритм 2011: Раунд 1 |
|---|
| Закончено |
В одном небезызвестном алгоритме нахождения k-порядковой статистики нужно разбить все элементы на пятерки подряд идущих элементов и найти медиану каждой пятерки. Медианой называют средний элемент отсортированного массива (для пятерки — это третий по величине элемент). Для оценки скорости работы этого алгоритма на современной видеокарте требуется уметь находить сумму медиан в каждой пятерке упорядоченного множества.
Суммой медиан отсортированного k-элементного множества S = {a1, a2, ..., ak}, где a1 < a2 < a3 < ... < ak, будем называть
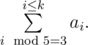
Оператор 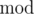 обозначает взятие остатка, то есть
обозначает взятие остатка, то есть 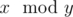 обозначает остаток при делении x на y.
обозначает остаток при делении x на y.
Для проведения нагрузочного тестирования потребовалось быстро вычислять сумму медиан для изменяющегося множества.
В первой строке задано число n (1 ≤ n ≤ 105) — количество операций, производимых с множеством.
Далее в каждой из n строк описана одна из трех операций:
- add x — добавить в множество элемент x;
- del x — удалить из множества элемент x;
- sum — найти сумму медиан множества.
Для любой операции add x верно, что элемент x непосредственно перед операцией не входит в множество.
Для любой операции del x верно, что элемент x непосредственно перед операцией входит в множество.
Все числа во входных данных — положительные целые числа, не превосходящие 109.
Для каждой операции sum выведите на отдельной строке сумму медиан текущего множества. Если множество пусто, то выведите 0.
Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать потоки cin, cout (также вы можете использовать спецификатор %I64d).
6
add 4
add 5
add 1
add 2
add 3
sum
3
14
add 1
add 7
add 2
add 5
sum
add 6
add 8
add 9
add 3
add 4
add 10
sum
del 1
sum
5
11
13
| Название |
|---|




