| AIM Tech Round 4 (Div. 1) |
|---|
| Закончено |
Дан ориентированный граф, состоящий из n вершин и m ребер, с выделенными вершинами s и t. При этом, в вершину s не входит ни одного ребра, а из вершины t не выходит ни одного ребра.
Изначально у каждого ребра была целая пропускная способность ci > 0. В сети с истоком s и стоком t был построен некоторый максимальный поток, и на ребре номер i записали fi — сколько единиц потока течет по этому ребру. Затем все пропускные способности ci и величины fi потока стерли, оставив лишь направление ребра и индикаторы gi: течет ли по ребру поток, т.е. 1, если fi > 0, и 0 иначе.
По графу и индикаторам gi определите, каково минимально возможное число насыщенных ребер в этой сети (ребро i является насыщенным, если fi = ci), и постройте соответствующую сеть c максимальным потоком в ней.
Поток в ориентированном графе задается величинами потока fi на каждом ребре такими, что выполняются условия:
- для каждой вершины, кроме истока и стока, сумма потока на входящих и выходящих из нее ребрах одинакова
- для каждого ребра 0 ≤ fi ≤ ci
Максимальный поток — такой поток, в котором разность между суммой величин потоков на ребрах, выходящих из истока, и суммой величин потоков на ребрах, входящих в исток (таких в этой задаче нет), максимальна.
Первая строка входных данных содержит целые числа n, m, s, t (2 ≤ n ≤ 100, 1 ≤ m ≤ 1000, 1 ≤ s, t ≤ n, s ≠ t) — количество вершин, количество ребер, номер истока и номер стока соответственно.
Каждая из следующих m строк входных данных содержит целые числа ui, vi, gi (1 ≤ ui, vi ≤ n, 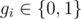 ) — начало ребра номер i, конец ребра номер i, и индикатор, равный 1, если по i-му ребру текла хотя бы одна единица потока, и 0 иначе.
) — начало ребра номер i, конец ребра номер i, и индикатор, равный 1, если по i-му ребру текла хотя бы одна единица потока, и 0 иначе.
Гарантируется, что никакое ребро не соединяет вершину саму с собой; что между каждой упорядоченной парой вершин не больше одного ребра; что существует хотя бы одна сеть и максимальный поток в ней, удовлетворяющие входным данным.
В первой строке выведите целое число k — минимальное число ребер, которые должны быть насыщены в максимальном потоке.
В каждой из следующих m строк выведите два целых числа fi, ci (1 ≤ ci ≤ 109, 0 ≤ fi ≤ ci) — поток по ребру номер i и пропускную способность ребра номер i. Эти данные должны задавать корректный максимальный поток в сети с такими пропускными способностями, ровно для k ребер должно выполняться fi = ci, а также fi > 0 должно выполняться тогда и только тогда, когда во входных данных для gi = 1.
Если возможных ответов несколько, выведите любой из них.
5 6 1 5
1 2 1
2 3 1
3 5 1
1 4 1
4 3 0
4 5 1
2
3 3
3 8
3 4
4 4
0 5
4 9
Иллюстрация к примеру из условия. Темным обозначены насыщенные ребра, пунктиром — ребро, по которому не идет поток (gi = 0). Число на ребре — номер данного ребра в списке. 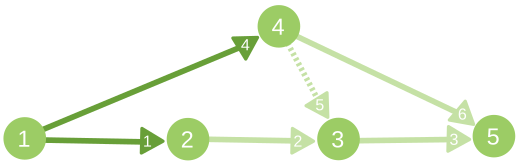
| Название |
|---|




