| AIM Tech Round 4 (Div. 1) |
|---|
| Закончено |
Дан взвешенный ориентированный граф, состоящий из n вершин и m ребер. Требуется ответить на q запросов двух типов:
- 1 v — найти длину кратчайшего пути из вершины 1 в вершину v.
- 2 c l1 l2 ... lc — прибавить 1 к весам ребер с номерами l1, l2, ..., lc.
Первая строка входных данных содержит целые числа n, m, q (1 ≤ n, m ≤ 105, 1 ≤ q ≤ 2000) — число вершин и ребер в графе и число запросов, соответственно.
Следующие m строк входных данных содержат описания ребер: в i-й из них находится описание ребра с номером i — три целых числа ai, bi, ci (1 ≤ ai, bi ≤ n, 0 ≤ ci ≤ 109) — начало ребра, конец ребра и его изначальный вес, соответственно.
Следующие q строк входных данных содержат описания запросов в вышеописанном формате (1 ≤ v ≤ n, 1 ≤ lj ≤ m). Гарантируется, что внутри одного запроса все lj различны, а также что суммарное число ребер в запросах второго типа не превосходит 106.
Для каждого запроса первого типа выведите строку с одним числом — длиной кратчайшего пути от 1 до v, либо -1, если такого путь не существует.
3 2 9
1 2 0
2 3 0
2 1 2
1 3
1 2
2 1 1
1 3
1 2
2 2 1 2
1 3
1 2
1
0
2
1
4
2
5 4 9
2 3 1
2 4 1
3 4 1
1 2 0
1 5
1 4
2 1 2
2 1 2
1 4
2 2 1 3
1 4
2 1 4
1 4
-1
1
2
3
4
Иллюстрация изменений графа в первом примере из условия:
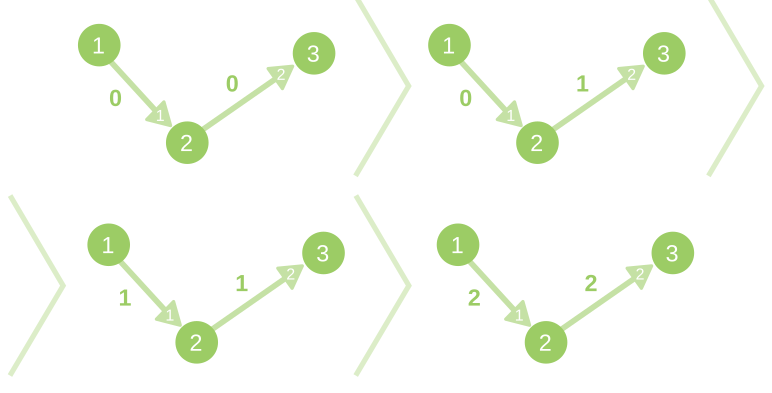
Иллюстрация изменений графа во втором примере из условия:
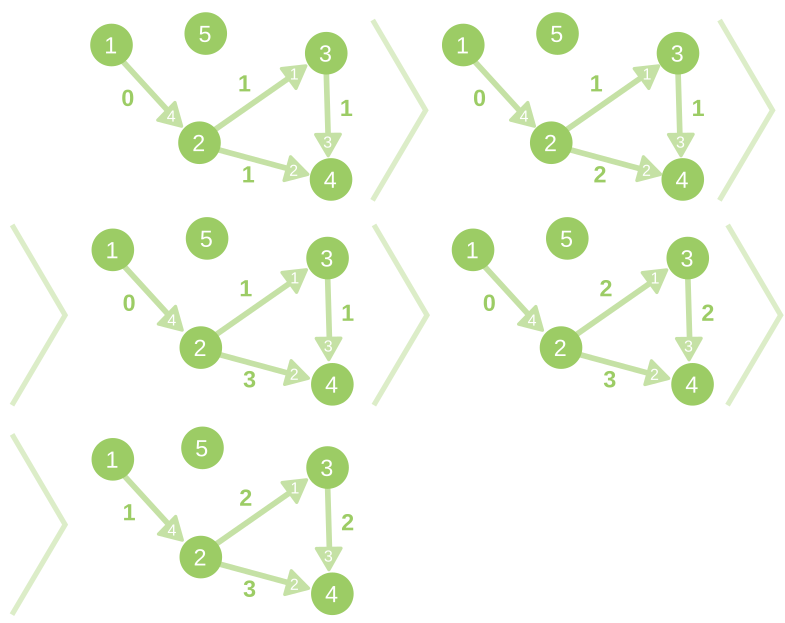
| Название |
|---|




