Аркадию снова требуется ваша помощь! Он решил построить свою высокоскоростную точку обмена трафиком. Она будет состоять из n узлов, соединенных в единую сеть минимально возможным количеством прямых кабелей (один кабель напрямую соединяет два узла). Из этих узлов ровно k будут точками подключения, и таким образом будут соединены только с одним другим узлом, а остальные будут соединены хотя бы с двумя другими узлами, таким образом обеспечивая надежную связь между точками подключения.
Аркадий хочет, чтобы задержки при передаче сигналов были как можно меньше, а для этого он хочет минимизировать расстояние между двумя самыми далекими точками подключения. Расстоянием Аркадий называет минимальное количество кабелей, по которым должен пройти пакет информации, чтобы добраться от одной точки подключения до другой.
Помогите Аркадию найти такой способ подключения узлов, при котором расстояние между двумя самыми далекими точками подключения минимально.
В первой строке находятся два целых числа n и k (3 ≤ n ≤ 2·105, 2 ≤ k ≤ n - 1) — общее количество узлов и количество точек подключения.
Обратите внимание, что при данных ограничениях всегда возможно построить хотя бы одну сеть из n узлов, имеющую ровно k точек подключения.
В первую строку выведите минимально возможное расстояние между двумя самыми далекими точками подключения. В следующих n - 1 строках выведите по два целых числа — номера узлов, соединенных очередным кабелем. Описание каждого кабеля должно быть выведено ровно один раз. Вы можете выводить описания кабелей и концы кабелей в любом порядке. Узлы сети нумеруйте с 1 до n. Аркадий сам поймет, какие из узлов будут являться точками подключения, поэтому они могут иметь любые номера.
Если ответов несколько, Аркадия устроит любой из них.
3 2
2
1 2
2 3
5 3
3
1 2
2 3
3 4
3 5
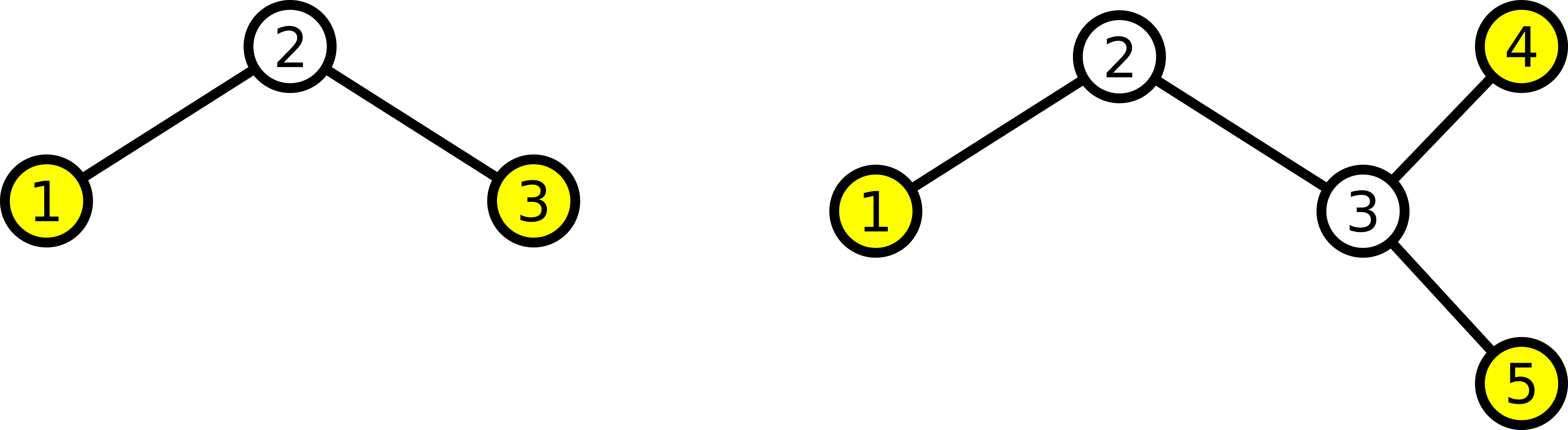
В первом примере единственно возможная сеть имеет вид, показанный на левом рисунке.
Во втором примере одна из оптимальных сетей показана на втором рисунке.
Узлы, являющиеся точками подключения, выделены желтым.
| Название |
|---|




