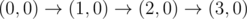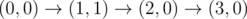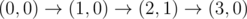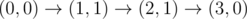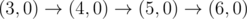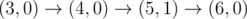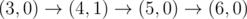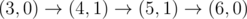| Codeforces Round 420 (Div. 2) |
|---|
| Закончено |
Окабэ любит гулять, но знает, что шпионы из Организации могут быть где угодно, поэтому он хочет узнать, по скольким различным путям он может пройти по городу. Город Окабэ состоит из всех точек (x, y) на плоскости таких, что x и y неотрицательны. Окабэ должен начать прогулку в начале координат (точке (0, 0)) и должен закончить путь в точке (k, 0). Если Окабэ сейчас находится в точке (x, y), то за один шаг он может перейти в точку (x + 1, y + 1), (x + 1, y) или (x + 1, y - 1).
Кроме того, существуют n горизонтальных отрезков, i-й из которых идет от точки x = ai до x = bi, включительно и располагается в y = ci. Гарантируется, что a1 = 0, an ≤ k ≤ bn, и ai = bi - 1 для всех 2 ≤ i ≤ n. i-й из этих отрезков заставляет Окабэ находиться только в точках с y координатой в отрезке 0 ≤ y ≤ ci, когда его x координата находится в отрезке ai ≤ x ≤ bi. Заметьте, что когда один отрезок кончается, а другой начинается, то он должен находиться под обоими отрезками одновременно.
Окабэ хочет узнать, сколько существует различных путей (последовательностей шагов) из начала координат в точку (k, 0), удовлетворяющих этим ограничениям, по модулю 109 + 7.
Первая строка содержит два целых числа n и k (1 ≤ n ≤ 100, 1 ≤ k ≤ 1018) — число отрезков и x координата точки назначения.
Следующие n строк содержат по три целых числа ai, bi и ci (0 ≤ ai < bi ≤ 1018, 0 ≤ ci ≤ 15) — левый и правый концы отрезка, и его y координата.
Гарантируется, что a1 = 0, an ≤ k ≤ bn, и ai = bi - 1 для всех 2 ≤ i ≤ n.
Выведите число путей, удовлетворяющих ограничениям, по модулю 1000000007 (109 + 7).
1 3
0 3 3
4
2 6
0 3 0
3 10 2
4

Рисунок выше соответствует первому примеру. Возможные пути следующие:

Рисунок выше соответствует второму примеру. Существует единственный способ до (3, 0). После этого возможные пути следующие:
| Название |
|---|