| Codeforces Round 420 (Div. 2) |
|---|
| Закончено |
Окабэ зачем-то нужны бананы для одного из экспериментов. Поэтому он решил сходить в лес и срубить банановых деревьев.
Рассмотрим точку (x, y) на плоскости такую, что x и y — целые числа, и 0 ≤ x, y. В такой точке растет дерево с x + y бананами на нем. В других точках нет деревьев. Окабэ нарисовал прямую, имеющую уравнение 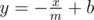 . Окабэ может выбрать один прямоугольник со сторонами, параллельными осям координат, такой, что все его точки лежат под или на прямой, и срубить все деревья внутри и на границе прямоугольника, собрав все бананы с них.
. Окабэ может выбрать один прямоугольник со сторонами, параллельными осям координат, такой, что все его точки лежат под или на прямой, и срубить все деревья внутри и на границе прямоугольника, собрав все бананы с них.
Помогите Окабэ найти максимальное число бананов, которое он может получить, если мудро выберет прямоугольник.
Окабе уверен, что ответ не превосходит 1018. Вы можете доверять ему.
Первая строка содержит два целых числа m и b (1 ≤ m ≤ 1000, 1 ≤ b ≤ 10000).
Выведите максимальное число бананов, которое может получить Окабэ с деревьев, которые он срубит.
1 5
30
2 3
25
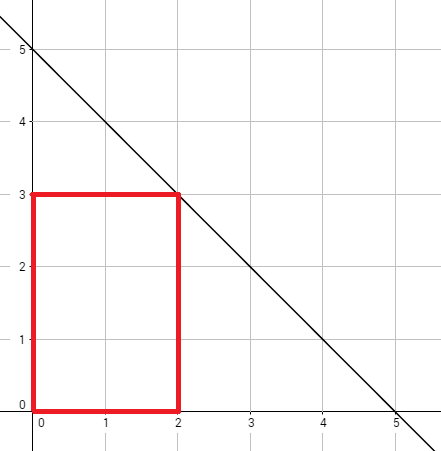
Рисунок выше соответствует первому примеру. Оптимальный прямоугольник показан красным, в нем находится 30 бананов.
| Название |
|---|




